Теорема Шаля. Положим, что отрезок, соединяющий точки А и В плоской фигуры, в два различных момента времени занимает на плоскости положения АВ и А1В1

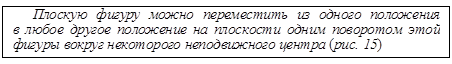
Рис. 15

Положим, что отрезок, соединяющий точки А и В плоской фигуры, в два различных момента времени занимает на плоскости положения АВ и А₁В₁. Разделим отрезок АА₁и ВВ₁ пополам. Из середин этих отрезков D и Е восстановим перпендикуляры к отрезкам и продолжим их до пересечения в точке P. Покажем, что эта точка неподвижной плоскости является центром поворота для данного конечного перемещения плоской фигуры. 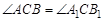по трем сторонам, отсюда имеем 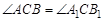. 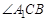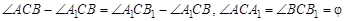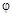Отняв от обеих частей этого равенства , получим , где – абсолютная величина рассматриваемого угла. Таким образом, перемещения двух точек фигуры, и, следовательно, всей плоской фигуры из первого положения во второе можно осуществить поворотом на угол 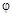вокруг центра поворота P. Поворот плоской фигуры как целого позволяет переместить эту фигуру из первого положение во второе.

Если перпендикуляры, восстановленные из середин отрезков, сливаются, то центр поворота лежит на пересечении продолжений отрезков АВ и А₁В₁.

5.2. Аналитический способ задания
плоского движения