Теорема о конечном перемещении плоской фигуры

Докажем, ч

Рис. 14

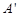Возьмем за полюс на рис. 14 точку А и переместим прямоугольник поступательно вместе с полюсом А. Тогда он займет следующее положение, а потом развернем плоскую фигуру на угол вокруг некоторой оси, проходящей через точку и перпендикулярной плоскости фигуры.

Возьмем за полюс другую точку, например точку , и переместим поступательно прямоугольник вместе с точкой , затем развернем ее на угол вокруг оси, проходящей через точку и перпендикулярно плоскости фигуры. Заметим, что . Но так как , то

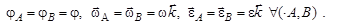
Здесь 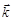перпендикулярно к плоскости фигуры.

Представив конечное перемещение плоской фигуры как последовательную совокупность бесконечно малых, приходим к выводу о том, что плоское движение твердого тела имеет три степени свободы: две поступательные с полюсом и одну вращательную вокруг мгновенной оси, проходящей через полюс: .