Обчислення. Підставляючи значення , і r у формулу (2), одержуємо
Підставляючи значення 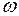 ,
, 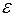 і r у формулу (2), одержуємо
і r у формулу (2), одержуємо
 = 1,65 м/с2.
= 1,65 м/с2.
Відповідь:a = 1,65 м/с2.
Приклад 4. На тіло масою 100 кг, що лежить на похилій площині, яка утворює кут 400 з горизонтом, діє горизонтальна сила 1500 Н (рис. 1.3). Визначити прискорення, з яким рухається тіло, якщо коефіцієнт тертя дорівнює 0,1.
Дано: m = 100 кг; F = 1500 Н; 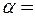 400; 400; 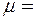 0,1.
Знайти: a.
Розв’язок.Виберемо напрямок координатних осей так, щоб одна з них була спрямована уздовж похилої площини (Ox), а інша – перпендикулярно до неї (Oy).
На тіло діють сила F – паралельно до основи похилої площини, сила ваги mg – вертикально вниз, реакція 0,1.
Знайти: a.
Розв’язок.Виберемо напрямок координатних осей так, щоб одна з них була спрямована уздовж похилої площини (Ox), а інша – перпендикулярно до неї (Oy).
На тіло діють сила F – паралельно до основи похилої площини, сила ваги mg – вертикально вниз, реакція
|  Рис. 1.3.
Рис. 1.3.
|
опори Q – перпендикулярно до похилої площини, і сила тертя Fтр – уздовж похилої площини вбік, протилежний рухові.
Запишемо другий закон Ньютона у векторній формі
 . (1)
. (1)
Для переходу до скалярної форми знайдемо проекції всіх діючих сил на координатні осі. Складові сили F на осі координат дорівнюють
 ;
; 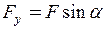 . (2)
. (2)
Складові сили ваги mg на осі координат дорівнюють
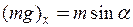 ;
; 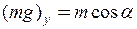 . (3)
. (3)
Сила Q діє тільки уздовж осі Oy, а сила тертя Fтер – протилежно до осі Ox.
Оскільки в напрямку Oy складова прискорення дорівнює нулю, з (1) – (3) виходить
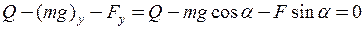 . (4)
. (4)
Проекція рівняння (1) на вісь (Ox) у цьому випадку має вид
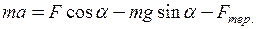 . (5)
. (5)
Сила тертя дорівнює добуткові сили нормального тиску тіла N на коефіцієнт тертя 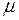
 . (6)
. (6)
Оскільки сила N за третім законом Ньютона дорівнює силі Q
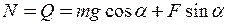 . (7)
. (7)
Таким чином, з (5)–(7) можна одержати остаточний вираз для прискорення a
 . (8)
. (8)
Дата добавления: 2015-09-28; просмотров: 791;
