Движение материальной точки по неподвижной кривой

Будем считать, что кривая, по которой движется материальная точка, задана. Примером такого движения точки может служить бусинка, движущаяся по проволоке. Для произвольного момента времени изобразим точку М в текущем положении (рис.11.2).

Рис.11.2

Применим естественный способ задания движения точки. Построим естественный трёхгранник МТNB и направим по направлениям Т, N, B единичные векторы .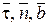

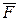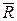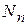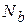Пусть - активная сила, действующая на точку, - реакция связи. Обозначим R_t - проекцию реакции связи на касательную, а проекции реакции на нормаль и бинормаль обозначим для удобства и соответственно. Тогда

,

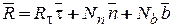Запишем основное уравнение динамики несвободной точки.

.

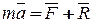Спроектируем его на естественные оси:

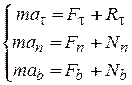(11.6)

Пусть точка О – начало отсчёта дуги s на траектории точки. Тогда 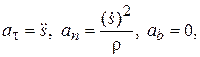где 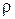- радиус кривизны траектории в точке М.

Подставляя проекции ускорения в уравнения (11.6), получим:

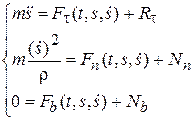(11.7)

Система уравнений (11.7) имеет четыре неизвестных:

.

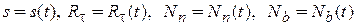Для того, чтобы система была замкнутой необходимо сделать одно дополнительное предположение. Наложим условия на силу трения .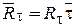

Рассмотрим три модели для силы трения.