ДИНАМИКА НЕСВОБОДНОГО ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ

Если точка во всё время движения (независимо от действующих сил) вынуждена двигаться по поверхности, либо по линии, либо в ограниченной области пространства, то она называется несвободной, а её движение несвободным.

Рис.11.1

Рассмотрим движение материальной точки M, находящейся на конце нерастяжимого стержня длиной l, другой конец которого закреплён с помощью шарнира в точке О (рис.11.1). При любых силах, приложенных к материальной точке, она совершает движение по поверхности сферы, радиус которой равен длине стержня. Координаты точки не будут независимыми, так как они должны удовлетворять уравнению сферы:

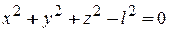. (11.1)

Ограничения, благодаря которым материальная точка вынуждена совершать несвободное движение, называются связями. Это понятие уже встречалось в статике. При изучении несвободного движения пользуются также знакомым из курса статики принципом освобождаемости от связей, а именно при рассмотрении несвободного движения следует действие связей на материальную точку заменить реакциями этих связей и рассмотреть материальную точку как свободную, но находящуюся под действием, как активных сил, так и реакций связей.

Уравнения линии или поверхности, по которым совершает движение точка, называются уравнениями связей. Примером уравнения связи, когда точка движется по поверхности, является уравнение (11.1). Если материальная точка движется по линии, то уравнения связи можно представить в виде

,

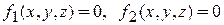т.е. в виде уравнений поверхностей, линией пересечения которых является траектория точки.

Если точка принуждена оставаться в некоторой области пространства, то уравнение свяиь аналитически задаётся в виде неравенства. Например, если в вышеуказанном случае (рис.11.1) заменить стержень нитью, уравнение связи будет иметь вид:

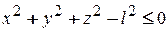(11.2)

Такая связь называется неудерживающей. Если точка, благодаря связи вынуждена оставаться на поверхности, либо на линии, то такая связь называется удерживающей. Уравнение связи в этом случае записывается в виде равенства. Таким образом, связь в первом случае (рис.11.1) является удерживающей.

Если время t явно не входит в уравнение связи, то связь называется стационарной. В примерах (11.1), (11.2) связи являются стационарными.

Если время t входит явно в уравнение связи, то связь называется нестационарной. Например, если в вышеуказанном случае (11.1) стержень втягивать, то уравнение связи будет иметь вид:

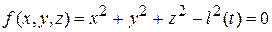. (11.3)

Связи делятся также на геометрические и кинематические. Когда уравнения связывают координаты точки, связь называют геометрической. В приведённых примерах (11.1), (11.2), (11.3) связи являются геометрическими. Если уравнения связывают кроме координат также и скорость (проекции скорости) точки, то такие связи называются кинематическими:

.

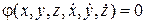При движении точки по поверхности, либо по линии реакцию связи можно разложить на касательную и нормальную составляющие. Касательная составляющая представляет собой силу трения. Связи без трения, реакции которых не имеют касательных составляющих, называются идеальными связями.