Замечания
1. Ускорения, которые фигурируют в аксиомах А2 и А4 являются абсолютными ускорениями.
2. Аксиомы А1 – А4 справедливы для свободной материальной точки.
Материальная точка называется свободной, если её перемещения не ограничены другими телами (связями).
Дифференциальные уравнения движения свободной материальной точки
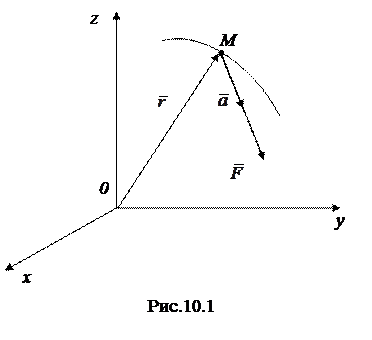 Пусть Oxyz – инерциальная система отсчета (ИСО). В ИСО справедливы аксиомы А1 и А2:
Пусть Oxyz – инерциальная система отсчета (ИСО). В ИСО справедливы аксиомы А1 и А2:
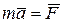 . (10.1)
. (10.1)
Учитывая, что по определению ускорение точки равно 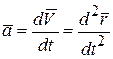 и подставляя это выражение в формулу (10.1), получим
и подставляя это выражение в формулу (10.1), получим
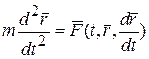 . (10.2)
. (10.2)
В уравнении (10.2) допускается, что сила может зависеть от времени 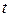 , положения (определяется радиус-вектором
, положения (определяется радиус-вектором 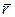 ) и скорости
) и скорости 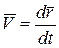 .
.
Получили, что радиус-вектор 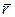 в каждый момент времени является содержимым дифференциального уравнения. Таким образом, формула (10.2) определяет дифференциальное уравнение движения свободной материальной точки в векторной форме.
в каждый момент времени является содержимым дифференциального уравнения. Таким образом, формула (10.2) определяет дифференциальное уравнение движения свободной материальной точки в векторной форме.
Дифференциальные уравнения движения свободной материальной точки в координатной форме
Проектируя уравнение (10.2) на оси ИСО Oxyz, получим
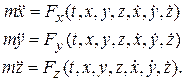 (10.3)
(10.3)
В этих уравнениях x, y, z - это координаты движущейся точки М (проекции радиус-вектора 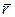 ),
), 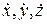 - проекции вектора
- проекции вектора 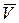 скорости точки,
скорости точки, 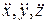 - проекции вектора
- проекции вектора 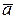 ускорения точки на оси системы координат Oxyz.
ускорения точки на оси системы координат Oxyz.
Уравнения (10.3) являются дифференциальными уравнениями движения свободной материальной точки в координатной форме.
Естественные уравнения движения свободной материальной точки
Введем вместо декартовых осей естественные оси 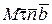 на траектории точки в каждый момент времени и спроектируем на них основной закон динамики (10.1):
на траектории точки в каждый момент времени и спроектируем на них основной закон динамики (10.1):
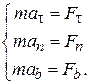 (10.4)
(10.4)
Учитывая, что касательное ускорение 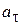 , нормальное ускорение
, нормальное ускорение 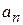 и бинормальное ускорение
и бинормальное ускорение 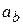 точки равны
точки равны
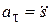 ,
, 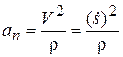 ,
, 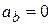 ,
,
где s – дуга, определяемая положение точки М на траектории, r - радиус кривизны траектории в текущем положении точки М, получим
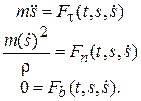 (10.5)
(10.5)
Уравнения (10.5) являются дифференциальными уравнениями движения материальной точки в естественной форме. Их также называют уравнениями в форме Эйлера.
Основные задачи динамики свободной материальной точки
Выделяют две основные задачи динамики свободной материальной точки:
1. Прямая задача.
Считая заданным движение материальной точки массой m, например, в векторной форме 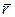 =
= 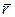 (t), определить равнодействующую сил
(t), определить равнодействующую сил 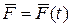 , вызывающих это движение.
, вызывающих это движение.
Чтобы решить эту задачу, нужно определить ускорение 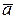 точки, продифференцировав дважды заданный закон движения точки
точки, продифференцировав дважды заданный закон движения точки
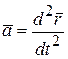
и подставить его в основной закон динамики:
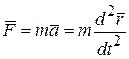 .
.
Таким образом, прямая задача всегда решается до конца.
Пример. Пусть уравнения движения точки заданы координатным способом:
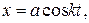
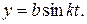 Определить
Определить 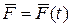 .
.
Решение. Траекторией точки является эллипс:
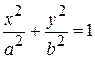 .
.
Из уравнений (10.3) 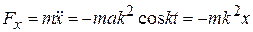 ;
;
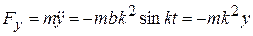 ;
;
Разложим вектор силы по ортам осей x и y:
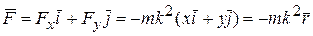 . (10.6)
. (10.6)
Из формулы (10.6) видно, что сила 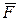 будет всегда направлена вдоль радиус-вектора точки
будет всегда направлена вдоль радиус-вектора точки 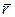 в противоположную ему сторону.
в противоположную ему сторону.
По модулю сила равна
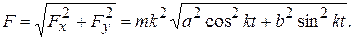
2. Обратная задача. ( Основная задача динамики свободной точки).
Определить движение, которое будет совершать точка массой 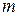 , под действием заданных сил, равнодействующая которых равна
, под действием заданных сил, равнодействующая которых равна 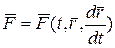 .
.
Решение. Используем уравнения (10.3)
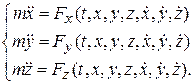
Чтобы решить обратную задачу нужно найти решение дифференциальных уравнений (10.3), т.е. проинтегрировать их. Аналитически эта задача решается только в частных случаях. Если аналитическое решение системы (10.3) невозможно, оно решается численно.
Если систему уравнений (10.3) удастся один раз проинтегрировать, то полученные новые зависимости будут включать время, координаты, их первые производные и три константы интегрирования С1, С2, С3:
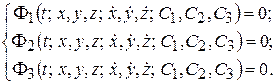 (10.6)
(10.6)
Систему (10.6) называют системой первых интегралов уравнений динамики точки.
Если систему (10.6) удастся проинтегрировать еще раз, то полученное решение будет зависеть еще от 3-х констант интегрирования С4, С5, С6:
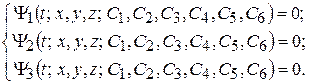 (10.7)
(10.7)
Для определения констант интегрирования используют начальные условия, которые задают начальное положение точки 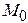 (
( 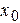 ,
, 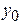 ,
, 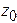 ) и ее начальную скорость
) и ее начальную скорость 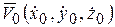 в момент времени t = t0:
в момент времени t = t0:
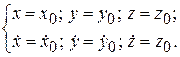 (10.8)
(10.8)
Подставляя начальные условия (10.8) в выражения (10.6) и (10.7), составляют шесть уравнений для определения констант интегрирования:
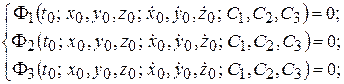
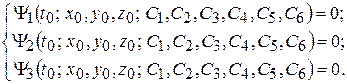
После определения констант интегрирования решение задачи, соответствующее заданным начальным условиям (10.8), записывается в виде:
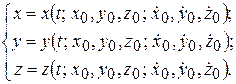
Пример. Задача Галилея
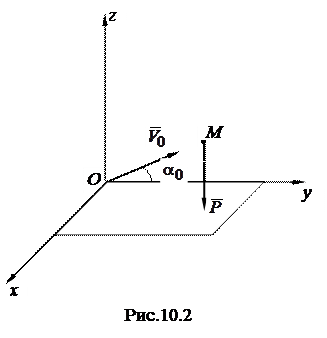
Рассмотрим движение тяжелой материальной точки в поле постоянной силы тяжести, брошенной с начальной скоростью 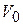 под углом
под углом 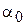 к горизонту.
к горизонту.
Будем считать, что плоскость 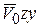 совпадает с плоскостью бросания в момент времени
совпадает с плоскостью бросания в момент времени 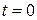 (рис. 10.2).
(рис. 10.2).
Дано: 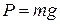 . Начальные условия: При
. Начальные условия: При 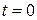 :
: 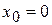 ,
, 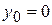 ,
, 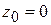 ,
, 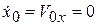 ,
, 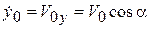 ,
, 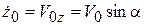 .
.
Найти 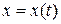 ,
, 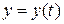 ,
, 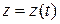 .
.
Решение. Основное уравнение динамики свободной материальной точки запишется в виде
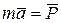 . (10.9)
. (10.9)
Проектируя уравнение (10.9) на оси 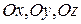 , получим систему дифференциальных уравнений:
, получим систему дифференциальных уравнений:
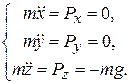 (10.10)
(10.10)
Разделяя переменные и сокращая на 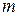 ,получим:
,получим:
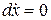 ,
, 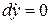 ,
, 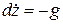 . (10.11)
. (10.11)
 Интегрируя уравнения (10.11), будем иметь
Интегрируя уравнения (10.11), будем иметь
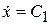 ,
, 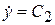 ,
, 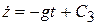 , (10.12)
, (10.12)
где 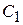 ,
, 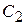 ,
, 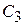 - константы интегрирования.
- константы интегрирования.
Подставляя в уравнения (10.12) начальные условия, получим
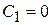 ,
, 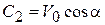 ,
, 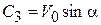 .
.
Следовательно, имеем
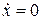 ,
, 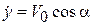 ,
, 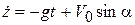 . (10.13)
. (10.13)
Вновь разделяя переменные в уравнениях(10.13) и интегрируя, получим
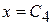 ,
, 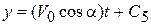 ,
, 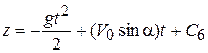 .
.
Используя начальные условия 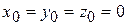 , определим константы интегрирования
, определим константы интегрирования 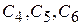 :
:
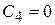 ,
, 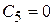 ,
, 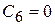 .
.
Следовательно, закон движения точки имеет вид:
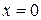 ,
, 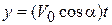 ,
, 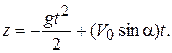
Из уравнений видно, что траекторией точки является плоская кривая (парабола), расположенная в вертикальной плоскости.
Дата добавления: 2015-09-21; просмотров: 954;
