Теорема Вариньона

Если система сил имеет равнодействующую, то момент равнодействующей относительно произвольной точки (либо оси) равен соответственно геометрической (или алгебраической) сумме моментов сил системы относительно той же точки (либо оси).

Дано: ,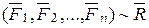

где 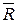- равнодействующая.

Доказать: 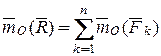, точка О - произвольная точка пространства

,

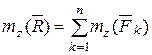где z - неподвижная ось.

Доказательство:

Воспользуемся вторым условием эквивалентности систем сил:

.

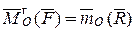По определению главного момента системы сил

.

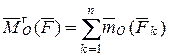Следовательно

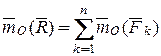. (4.8)

Проектируя (4.8) на ось z получим

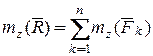. (4.9)

Теорема доказана.

На основании основной теоремы статики доказывается теорема о трех непараллельных силах также используемая при решении практических задач.