Теорема о трех непараллельных силах
Если под действием трех непараллельных сил твердое тело находится в равновесии, то все силы необходимо пересекаются в одной точке.
Доказательство:
Пусть даны три непараллельные силы 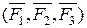 . Возьмем точку О, например, на линии действия силы
. Возьмем точку О, например, на линии действия силы 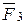 (рис.4.1)
(рис.4.1)
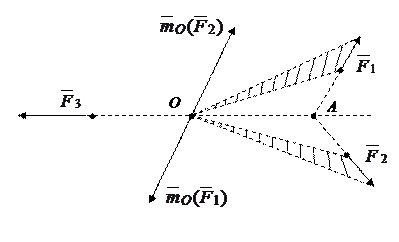
Рис.4.1
Тогда на основании основной теоремы статики
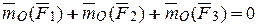 .
.
Так как 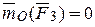 , то
, то 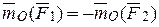 .
.
Следовательно силы 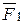 и
и 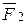 лежат в одной плоскости, проходящей через точку О и так как они не параллельны, то линии их действия пересекаются, пусть в точке А.
лежат в одной плоскости, проходящей через точку О и так как они не параллельны, то линии их действия пересекаются, пусть в точке А.
Заменив их на равнодействующую 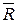 по аксиоме А1, получим, что линия действия силы
по аксиоме А1, получим, что линия действия силы 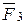 должна проходить через точку А.
должна проходить через точку А.
Теорема доказана.
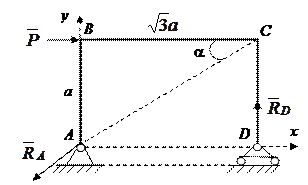 Рис.4.2
Рис.4.2
| Пример.Рама АВСD, изображенная на рис.4.2, концом А закреплена на неподвижной опоре цилиндрическим шарниром, а концом D положена на подвижный каток. Определить опорные реакции 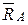 и и 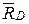 , возникающие при действии горизонтальной силы , возникающие при действии горизонтальной силы 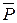 приложенной в точке В. Весом рамы пренебречь. приложенной в точке В. Весом рамы пренебречь.
|
Решение.Рама находится в равновесии под действием трех непараллельных сил 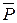 ,
, 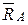 ,
, 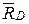 . Реакция подвижной опоры
. Реакция подвижной опоры 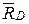 направлена по нормали к опорной поверхности. Линию действия реакции
направлена по нормали к опорной поверхности. Линию действия реакции 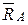 определим из теоремы о трех непараллельных силах, соединив точку А с точкой пересечения С силы
определим из теоремы о трех непараллельных силах, соединив точку А с точкой пересечения С силы 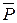 и реакции
и реакции 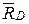 .
.
Определим угол a из прямоугольного треугольника АВС.
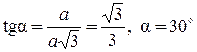 .
.
Зная угол a, реакции опор можно определить геометрически из силового треугольника (рис.4.3), либо аналитически, составив уравнения равновесия.
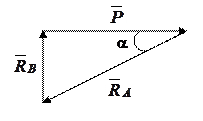 Рис.4.3
Рис.4.3
| Из прямоугольного силового треугольника 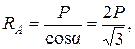 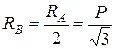 . .
|
Решим задачу, составив уравнения равновесия для плоской сходящейся системы сил, направив координатные оси согласно рис.4.2:
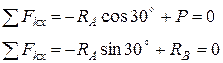 (4.10)
(4.10)
Из уравнений (4.10) 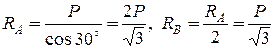 .
.
Дата добавления: 2015-09-21; просмотров: 1448;
