ТЕОРЕМА ОБ ЭКВИВАЛЕНТНОСТИ

Для эквивалентности двух систем сил необходимо и достаточно, чтобы были равны их главные векторы и главные моменты относительно любого произвольного центра.

Пусть имеем две системы сил

.

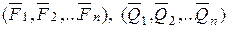Запишем теорему схематически.

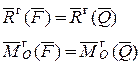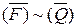
Достаточность Необходимость т.О - произвольная   Условие теоремы Утверждение теоремы

Докажем сначала необходимость .

Дано: .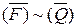

Доказать: 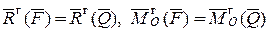, точка О - произвольная точка пространства.

Доказательство:

Из условия 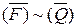по определению эквивалентности системы сил следует существование такой системы сил 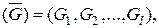что

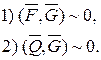
По основной теореме статики из первого условия следует

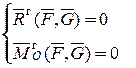. (4.1)

Из второго условия следует

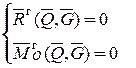. (4.2)

По определению

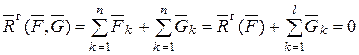(4.3)

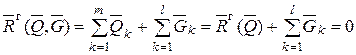(4.4)

Из формулы (4.3) и (4.4) следует

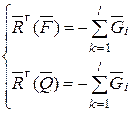(4.5.)

Сравнивая формулы (4.5), получим

.

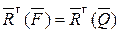Далее аналогично

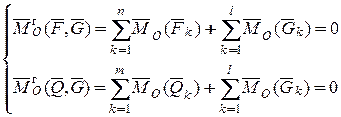(4.6)

Из формулы (4.6) следует

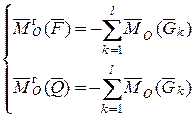(4.7)

Откуда

.

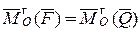Докажем достаточность.

Дано: 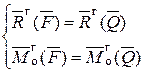, точка О - произвольная точка пространства.

Доказать: .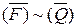

Доказательство:

Добавим к обеим системам систему сил 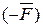с противоравными системе 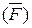силами:

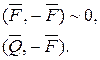
Найдем главный вектор и главный момент системы сил :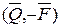

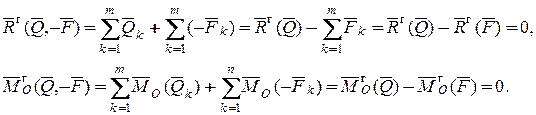
На основании основной теоремы статики

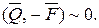
Но и .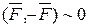

Следовательно, по определению эквивалентности систем сил

.

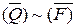Теорема доказана.

На практике при вычислениях моментов сил часто используется теорема Вариньона, которая непосредственно следует из теоремы эквивалентности.