Плоска хвиля
Рівняння плоскої хвилі має вигляд:
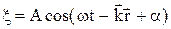 , (1)
, (1)
де 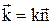 ¾ хвильовий вектор,
¾ хвильовий вектор, 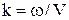 ¾ хвильове число,
¾ хвильове число, 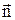 ¾ одиничний вектор нормалі до хвильового фронту.
¾ одиничний вектор нормалі до хвильового фронту.
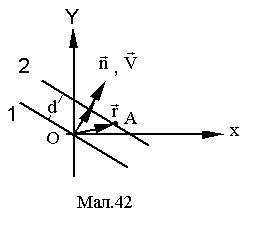
Дійсно, нехай джерелом коливань є нескінченно велика площина 1 (див. Мал. 42) із нормаллю 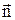 , що є хвильовим фронтом плоскої хвилі. Площина проходить через початок координат. Нехай рівняння коливання точок в площині 1 має вигляд
, що є хвильовим фронтом плоскої хвилі. Площина проходить через початок координат. Нехай рівняння коливання точок в площині 1 має вигляд
x=Acos(wt+a). (2)
Через час t' площина 1 переміститься на відстань d і займе положення 2. Відстань між площинами визначається скалярним добутком 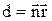 , де
, де 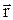 ¾ радіус-вектор деякої точки А на площині. Коливання в цій площині запізнюються на час
¾ радіус-вектор деякої точки А на площині. Коливання в цій площині запізнюються на час 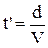 і будуть мати вигляд
і будуть мати вигляд
x = Acos(wt - wt' + a) = Acos(wt - w 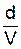 + a) = Acos(wt - kd + a). (3)
+ a) = Acos(wt - kd + a). (3)
 Тепер, позначивши
Тепер, позначивши 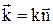 , можна записати:
, можна записати:
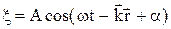 , (4)
, (4)
що й треба було довести.
Сферична хвиля. Рівняння сферичної хвилімає вигляд
y= 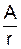 cos(wt-kr). (5)
cos(wt-kr). (5)
Амплітуда сферичної хвилі зменшується обернено пропорційно відстані r від джерела хвиль, а енергія обернено пропорційна квадратові відстані.
Циліндрична хвиля. Циліндрична хвиля описується рівнянням плоскої хвилі з обмеженим деякою плоскою поверхнею хвильовим фронтом.
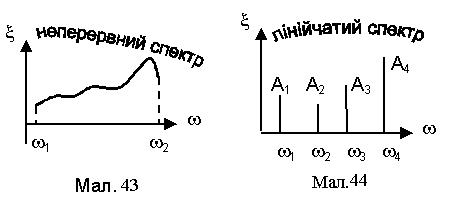 |
Спектр частот хвиль. Під частотним спектром хвилірозуміють сукупність частот, якими можна представити дану хвилю.
Хвиля з неперервним спектром частот ¾ хвиля, що містить значення частоти коливань в деякому неперервному інтервалі частот від w1 до w2 (див. Мал.43).
Хвиля з лінійчатим спектромчастот ¾ хвиля, що містить коливання дискретних значень частоти (див. Мал.44).
Дата добавления: 2015-09-18; просмотров: 1217;
