Однородная плоская стенка
Нахождение теплового потока в этом случае является простейшей задачей теории теплообмена.
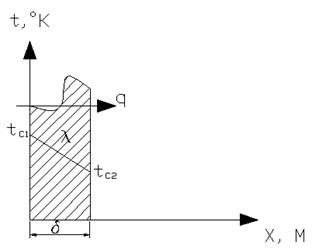
Рисунок 2.4 – Пример теплообмена однородной плоской стенки
Пусть имеем плоскую стенку неограниченных размеров. Толщина стенки 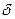 , материал имеет коэффициент теплопроводности
, материал имеет коэффициент теплопроводности 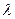 . Температура на поверхности
. Температура на поверхности 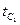 и
и  . Принимаем, что распределение температуры в стенке линейное. Температура изменяется только вдоль одной координаты x (одномерная задача). Требуется определить плотность теплового потока
. Принимаем, что распределение температуры в стенке линейное. Температура изменяется только вдоль одной координаты x (одномерная задача). Требуется определить плотность теплового потока 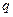 и уметь рассчитать распределение температуры по толщине стенки.
и уметь рассчитать распределение температуры по толщине стенки.
Запишем уравнение Фурье:
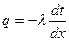 ,
, 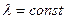 ,
,
тогда
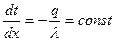 .
.
На практике коэффициент теплопроводности 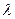 чаще всего определяют по справочнику для средней температуры, тогда:
чаще всего определяют по справочнику для средней температуры, тогда:
 .
.
Проинтегрируем последнее выражение:
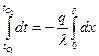 .
.
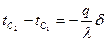 .
.
Тогда плотность теплового потока будет равна
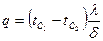 .
.
Откуда
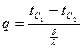 .
.
где 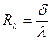 - тепловое сопротивление стенки.
- тепловое сопротивление стенки.
Тогда закон Фурье для определения плотности теплового потока q:
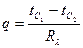 .
.
Закон Фурье для тонкой стенки аналогичен закону Ома:
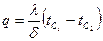 ;
;
где 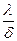 - тепловая проводимость.
- тепловая проводимость.
Иногда используется выражение для теплового сопротивления стенки в виде:
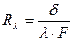 .
.
Тогда тепловой поток, прошедший через стенку будет равен
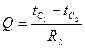 .
.
Дата добавления: 2015-09-11; просмотров: 1485;
