Побудова гістограми
1.5.1.1 Здійснюють спостереження за випадковою величиною і визначають її числові значення. Для того, аби отримати достатньо вірогідну гістограму, n–число експериментальних точок повинно бути не менш ніж 30.
Приклад. Виміримо коефіцієнт деформації металевого матеріалу у процесі термообробки і складемо таблицю його значень:
| 0,9 | 1,5 | 0,9 | 1,1 | 0,9 | 1,1 | 1,1 | 1,2 | ||
| 0,6 | 0,1 | 0,7 | 0,8 | 0,7 | 0,8 | 0,5 | 0,8 | 1,2 | 0,6 |
| 1,4 | 1,4 | 0,9 | 1,1 | 0,9 | 1,4 | 0,9 | 1,8 | 0,9 | 1,4 |
| 1,1 | 1,4 | 1,4 | 1,4 | 0,9 | 1,1 | 1,4 | 1,1 | 1,3 | 1,1 |
| 1,5 | 1,6 | 1,6 | 1,5 | 1,6 | 1,5 | 1,6 | 1,7 | 1,8 | 1,5 |
1.5.1.2 Визначають розмах R (розкид випадкової величини).Обираютьxmin та xmax (відповідно найменше і найбільше значення), R підраховують за рівнянням:
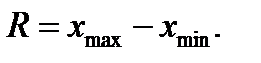 (1.8)
(1.8)
Розмах обумовлює ширину гістограми.
Для прикладу, що розглядається: 1,8 – максимальне значення; 0,1 – мінімальне значення; у результаті розмах складе 1,7.
1.5.1.3 Одержаний розмах R поділяють на декілька інтервалів (k). Ширину інтервалу визначають за рівнянням:
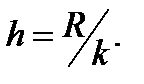 (1.9)
(1.9)
Кількість інтервалів k залежить від загального числа зібраних даних. Звичайно k =від 6 до 20 або 8–12. Для зручності бажано використовувати округлені числа. Для наведеного прикладу: кількість інтервалів 9, а ширина інтервалу складає 0,1889, або ~ 0,2.
1.5.1.4 Розподіляють одержані дані за інтервалами. Ліва межа 1-го інтервалу = xmin, права межа = xmin + h і т. д. визначають штриховими позначеннями кількість показників, що потрапили до кожного інтервалу, і заносять їх до спеціально підготовленого бланка реєстрації.
Бланк для наведеного прикладу має наступний вигляд:
| № за/п | Інтервали | Середина інтервалу | Штрихові позначення частоти | Частота | Накопичена частота |
| 0,05–0,25 0,25–0,45 0,45–0,65 0,65–0,85 0,85–1,05 1,05–1,25 1,25–1,45 1,45–1,65 1,65–1,85 | 0,15 0,35 0,55 0,75 0,95 1,15 1,35 1,55 1,75 | // ///// /// ///// ///// /// ///// ///// ///// ///// ///// ///// ///// ///// ///// ///// // ///// ///// /// ///// //// /// |
1.5.1.5 За одержаними даними будують гістограму. На осі ординат відкладають межі інтервалів, а вздовж осі абсцис – частоти.
Для нашого прикладу отримано гістограму, яку наведено на рисунку 1.5.
Рисунок 1.5 – Гістограма за результатами прикладу
1.5.1.6 За формою одержаної гістограми з’ясовують стан партії виробів, технологічного процесу, заходи, що вживалися.
На рисунку 1.6 наведені типові види гістограм, якими можна скористатися як зразками під час аналізу процесів: звичайний тип (а); гребінець (мультимодальний тип (б)); додатньо (від’ємно) скошений роподіл (в); розподіл з обривом зліва – справа (г); плато (д); двопіковий тип (е); розподіл з ізольованим піком (ж).
| а – звичайний тип (симетричний) б – гребінець (мультимодальний тип) |
| в – додатньо (від’ємно) скошений розподіл г – розподіл з обривом ліворуч (праворуч) |
| д – плато (равномірний і прямокутний розподіл) е – двопіковий (бімодальний) тип |
| ж – розподіл з ізольованим піком |
Рисунок 1.6 – Види гістограм (опис наведено у тексті)
Звичайний тип (симетричний) (див. рис. 1.6, а). Гістограма з таким розподілом зустрічається найчастіше. Вона вказує на стабільність процесу.
Гребінець (мультимодальний тип) (див. рис. 1.6, б). Класи через один мають нижчі частоти. Така форма зустрічається, коли кількість одиничних спостережень, які потрапляють у клас, коливається, або коли діє певне правило округлення даних.
Додатньо (від’ємно) скошений розподіл (див. рис. 1.6, в). Середнє значення гістограми локалізується зліва (справа) від центру розмаху.
Розподіл з обривом зліва (справа) (див. рис. 1.6, г). Це одна з форм, що часто зустрічається за 100 % -ого контролю виробів через погане відтворювання процесу, або за виключення з партії усіх виробів з параметрами нижче від контрольного нормативу (або вище, або й ті й інші).
Плато (равномірний прямокутний розподіл) (див. рис. 1.6, д). Така гістограма з’являється у випадках поєднання декількох розподілень, в яких середні значення відрізняються незначно. Аналіз такої гістограми доцільно здійснювати, використовуючи метод розшарування.
Двопіковий (бімодальний) тип (див. рис. 1.6, е). Така форма зустрічається, коли поєднуються два розподілення з суттєво віддаленими середніми значеннями, наприклад, за наявності різниці між двома видами матеріалів, двома операторами і т. ін. У цьому випадку можливо провести розшарування за двома видами чинників, дослідити причини відмінності і прийняти відповідні запобіжні заходи з усунення.
Розподіл з ізольованим піком (див. рис. 1.6, ж). Поряд з розподілом звичайного типу з’являється маленький ізольований пік, зазвичай за наявності дрібних включень даних з іншого розподілу або за появи помилки у вимірюванні. За результатами аналізу гістограми надають висновок про необхідність налагодження вимірювального приладу або термінового здійснення контролювання процесу.
Дата добавления: 2015-11-18; просмотров: 2416;
