Діаграма розкиду – інструмент, що дозволяє визначити вид і сенс зв’язку між парами відповідних змінних.
Діаграма розкиду, також як і метод розшарування (стратифікації), використовується для виявлення причинно-наслідкових зв’язків показників якості і впливу на них чинників під час аналізу причинно-наслідкової діаграми.
Діаграма розкиду являє собою графік, що виходить під час нанесення у відповідному масштабі експериментальних точок, які отримані у результаті спостережень. Координати точок відповідають значенням величини, що розглядається, та чинника впливу. Розміщення точок на графіку виявляє наявність і характер зв’язку між випадковими величинами. Таким чином, діаграма розкиду надає можливість висунути гіпотезу про наявність або відсутність кореляційного зв’язку між двома випадковими величинами, які можуть стосуватися характеристики якості і чинника, що впливає на неї, або двох різних характеристик якості, або двох чинників, які впливають на одну характеристику якості.
Діаграма будується як графік залежності між двома параметрами: вздовж горизонтальної осі відкладають обміри величин однієї змінної, вздовж вертикальної осі – іншої.
Можливі численні варіанти скупчення точок, деякі типові з них наведені на рисунку 1.4.
За наявності кореляційної залежності можливо здійснити контроль тільки однієї (будь-якої) з двох характеристик. При цьому характер кореляційної залежності, що визначається виглядом діаграми розкиду, надає уявлення про зміни одного з параметрів за певних змін іншого. Так, за збільшеня х на рисунку 1.4, а, у також буде збільшуватися (пряма кореляція). У цьому випадку за здійснення контролю причинних чинників х (відгуку) характеристика у (функція) буде залишатися стабільною.
| б |
| а |
| У |
| У |
| г |
| в |
Рисунок 1.4 – Типові види діаграми розкиду:
а – пряма кореляція; б – від’ємна кореляція; в – відсутність кореляції;
г – криволінійна кореляція
На рисунку 1.4, б показано приклад зворотньої (від’ємної) кореляції. За збільшення х характеристика у зменшується. Якщо причинний фактор х знаходиться під контролем, характеристика у залишається стабільною. На рисунку 1.4, в – приклад відсутності кореляції, коли ніякої виявленної залежності між х і у не спостерігається. У цьому випадку необхідно продовжити пошук чинників, корелюючих з у, виключивши з цього пошуку чинник х.
Між параметрами х і у можливі також випадки криволінійної кореляції (рис. 1.4, г). Якщо при цьому діаграму розкиду поділити на ділянки, що мають прямолінійний характер, то досліджують кожну ділянку окремо.
Бажано отримати кількісну оцінку щільності або міці звязку між величинами. Такою кількісною оцінкою є коефіцієнт кореляції rxy:
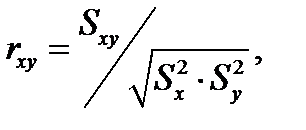(1.1)
де Sxy – коваріація випадкових величин х та у, що дорівнює:
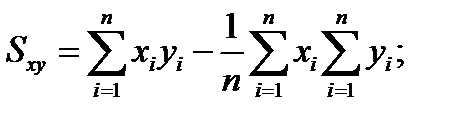(1.2)
Sx, Sy – вибіркові дисперсії величин х і у, що визначаються за формулами:
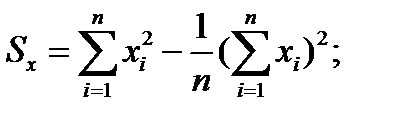(1.3)
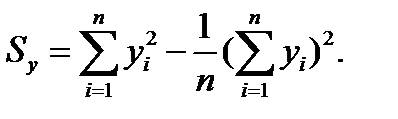(1.4)
Якщо r = 0, то зв'язок відсутній; якщо r близько до 1, то зв'язок позитивний; якщо r близько до – 1, то зв'язок від’ємний.
Для розрахунку коефіцієнта кореляції складається таблиця з наступними графами:
| № за/п | х | у | ху | х2 | у2 |
| … Сума Середнє |
Якщо виявляється, що між двома випадковими величинами існує зв'язок, то можна знайти математичний вираз залежності між ними – формулу, у якій кожному значенню однієї випадкової величини буде відповідати середнє значення іншої випадкової величини. Така залежність називається регресійною.
Розглянемо регресію, що найбільш часто зустрічається. Як відомо, рівняння має вигляд:
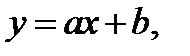(1.5)
де у – функція (залежна змінна), х – аргумент (незалежна змінна),
в – значення функції при х = 0, а – кутовий коефіцієнт прямої, що дорівнює зміні функції за зміни аргументу на одну одиницю (позитивний, якщо під час збільшення аргументу підвищується і значення функції, і від’ємний у протилежному випадку).
У випадку ймовірностної (стохастичної) залежності між випадковими величинами кожному значенню аргумента відповідає цілий діапазон зміни залежної величини. Тому залежну величину називають не функцією, а відгуком. Між аргументом і відгуком немає однозначного зв’язку, а є лише ймовірностний зв'язок, зв'язок у середньому, коли значенню аргументу можливо поставити у відповідність у якості найбільш ймовірного середнє значення іншої випадкової величини.
Лінії регресії визначають за експериментальними точками. Вона повинна проходити так, щоб бути найближче до цих точок, але при цьому залишатися прямою. Найбільш придатна – це лінія, у якій сума відхилень від експериментальних точок найменьша, тому бажано визначити її коефіцієнти. При цьому коефіцієнти а і в лінії регресії визначають із співвідношень:
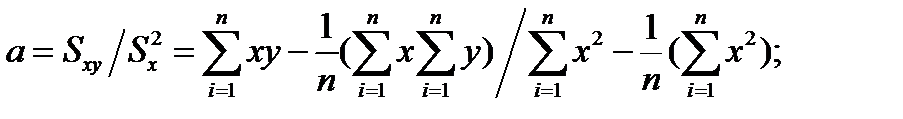(1.6)
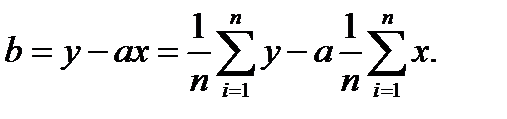(1.7)
Можна також визначити кут нахилу лінії регресії до осі х. Це кут a. У відповідному масштабі тангенс цього кута визначається як відношення зміни величини у до відповідної зміни аргументу х: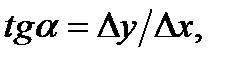 
який дорівнює а. Якщо а> 0, то зв'язок додатній; якщо а < 0, то зв'язок від’ємний.
ГІСТОГРАМА
Дата добавления: 2015-11-18; просмотров: 1948;