Задача квантовой механики о движении свободной частицы

Рассмотрим движение свободной частицы. Это означает, что ее потенциальная энергия .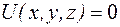

Пусть частица движется вдоль оси 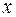. Тогда 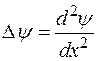и уравнение Шредингера для стационарных состояний будет иметь вид

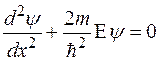. (1.5.1)

Обозначим 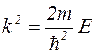. (1.5.2)

Здесь k- волновое число, или модуль волнового вектора. Тогда уравнение (1.5.1) будет иметь вид

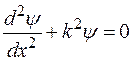. (1.5.3)

Решением уравнения (1.5.3) является функция вида

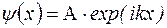. (1.5.4)

Её можно записать также в виде

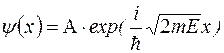. (1.5.5)

Функция 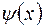, определяемая выражениями (1.5.4) и (1.5.5) представляет собой только координатную часть волновой функции. Зависящая от времени и координат волновая функция, описывающая движение свободной частицы будет иметь вид

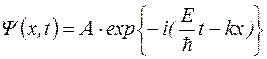(1.5.6)

Уравнение (1.5.6) есть не что иное, как уравнение плоской волны в комплексной форме. Волновая функция (1.5.6) описывает плоскую монохроматическую волну де Бройля.

Проведем анализ полученного решения.

Решение уравнения Шредингера для свободной частицы существует при любых значениях энергии и волнового числа. Это означает, что E и k могут изменяться непрерывно. Свободная частица имеет сплошной спектр энергии.

Найдем плотность вероятности обнаружения частицы

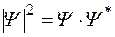(1.5.6)

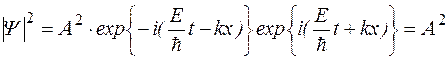(1.5.6)