Понятие о туннельном эффекте.

Туннельным эффектом называют прохождение частиц сквозь потенциальный барьер за счет волновых свойств частиц.

Пусть частица, движущаяся слева направо, встречает на своем пути потенциальный барьер высотой U₀ и шириной l. По классическим представлениям частица беспрепятственно проходит над барьером, если ее энергия E больше высоты барьера (E>U₀). Если же энергия частицы меньше высоты барьера (E<U₀), то частица отражается от барьера и начинает двигаться в обратную сторону, сквозь барьер частица проникнуть не может.

В квантовой механике учитываются волновые свойства частиц. Для волны левая стенка барьера – это граница двух сред, на которой волна делится на две волны – отраженную и преломленную. Поэтому даже при E>U₀ возможно (хотя и с небольшой вероятностью) отражение частицы от барьера, а при E<U₀ имеется отличная от нуля вероятность того, что частица окажется по другую сторону потенциального барьера. В этом случае частица как бы «прошла сквозь туннель».

Решим задачу о прохождении частицы сквозь потенциальный барьер для наиболее простого случая одномерного прямоугольного барьера, изображенного на рис.1.6. Форма барьера задается функцией

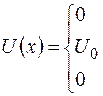
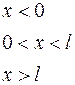. (1.7.1)

Запишем уравнение Шредингера для каждой из областей: 1(x<0), 2(0<x<l) и 3(x>l):

; (1.7.2)

; (1.7.3)

. (1.7.4)

Обозначим

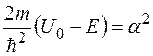(1.7.5)

и

. (1.7.6)

Общие решения уравнений (1), (2), (3) для каждой из областей имеют вид:

; (1.7.7)

; (1.7.8)

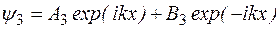. (1.7.9)

Решение вида соответствует волне, распространяющейся в направлении оси x, а 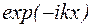- волне, распространяющейся в противоположном направлении. В области 1 слагаемое 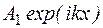описывает волну, падающую на барьер, а слагаемое - волну, отраженную от барьера. В области 3 (справа от барьера) имеется только волна, распространяющаяся в направлении x, поэтому .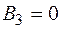

Волновая функция должна удовлетворять условию непрерывности, поэтому решения (6),(7),(8) на границах потенциального барьера необходимо «сшить». Для этого приравниваем волновые функции и их производные при x=0 и x = l:

; ;

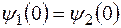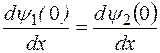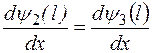; . (1.7.10)

Используя (1.7.7) - (1.7.10), получим четыре уравнения для определения пяти коэффициентов А₁ , А₂, А₃, В₁ и В₂:

А₁+В₁=А₂+В₂ ;

А₂еxp(a l) + В₂еxp(-a l)= А₃еxp(ikl) ;

ik(А₁– В₁) = a(А₂–В₂) ; (1.7.11)

a(А₂еxp(al)–В₂еxp(-al) = ik А₃еxp(ikl).

Чтобы получить пятое соотношение, введем понятия коэффициентов отражения и прозрачности барьера.

Коэффициентом отражения назовем отношение

, (1.7.12)

которое определяет вероятность отражения частицы от барьера.

Коэффициент прозрачности

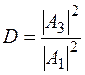(1.7.13)

дает вероятность того, что частица пройдет через барьер. Так как частица либо отразится, либо пройдет через барьер, то сумма этих вероятностей равна единице. Тогда

R+D =1; (1.7.14)

или

. (1.7.15)

Это и есть пятое соотношение, замыкающее систему (1.7.11), из которой находятся все пять коэффициентов.

Наибольший интерес представляет коэффициент прозрачности D. После преобразований получим

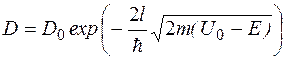, (7.1.16)

где D₀ – величина, близкая к единице.

Из (1.7.16) видно, что прозрачность барьера сильно зависит от его ширины l, от того, на сколько высота барьера U₀ превышает энергию частицы E, а также от массы частицы m.

С классической точки зрения прохождение частицы сквозь потенциальный барьер при E<U₀ противоречит закону сохранения энергии. Дело в том, что если классическая частица находилась бы в какой-то точке в области барьера (область 2 на рис. 1.7), то ее полная энергия оказалась бы меньше потенциальной энергии (а кинетическая – отрицательной!?). С квантовой точки зрения такого противоречия нет. Если частица движется к барьеру, то до столкновения с ним она имеет вполне определенную энергию. Пусть взаимодействие с барьером длится время Dt, тогда, согласно соотношению неопределенностей, энергия частицы уже не будет определенной; неопределенность энергии . Когда эта неопределенность оказывается порядка высоты барьера, он перестает быть для частица непреодолимым препятствием, и частица пройдет сквозь него.

Прозрачность барьера резко убывает с его шириной (см. табл. 1.1.). Поэтому частицы могут проходить за счет туннельного механизма лишь очень узкие потенциальные барьеры.

Таблица 1.1

Значения коэффициента прозрачности для электрона при (U₀ – E) = 5 эВ = const

Мы рассмотрели барьер прямоугольной формы. В случае потенциального барьера произвольной формы, например такой, как показано на рис.1.7, коэффициент прозрачности имеет вид

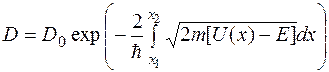. (1.7.17)

Туннельный эффект проявляется в ряде физических явлений и имеет важные практические приложения. Приведем некоторые примеры.

1. Автоэлектронная (холодная) эмиссия электронов.

В 1922 г. было открыто явление холодной электронной эмиссии из металлов под действием сильного внешнего электрического поля. График зависимости потенциальной энергии U электрона от координаты x изображен на рис. При x < 0 – область металла, в котором электроны могут двигаться почти свободно. Здесь потенциальную энергию можно считать постоянной. На границе металла возникает потенциальная стенка, не позволяющая электрону покинуть металл, он может это сделать, лишь приобретя добавочную энергию, равную работе выхода A. За пределами металла (при x > 0) энергия свободных электронов не меняется, поэтому при x > 0 график U(x) идет горизонтально. Создадим теперь вблизи металла сильное электрическое поле. Для этого возьмем металлический образец в форме острой иглы и подсоединим его к отрицательному полюсу источни Рис. 1.9 Принцип действия туннельного микроскопа

ка напряжения, (он будет катодом); поблизости расположим другой электрод (анод), к которому присоединим положительный полюс источника. При достаточно большой разности потенциалов между анодом и катодом можно создать вблизи катода электрическое поле с напряженностью порядка 10⁸ В/м. Потенциальный барьер на границе металл – вакуум становится узким, электроны просачиваются сквозь него и выходят из металла.

Автоэлектронная эмиссия использовалась для создания электронных ламп с холодными катодами (сейчас они практически вышли из употребления), в настоящее время она нашла применение в туннельных микроскопах, изобретенных в 1985 г. Дж. Биннингом, Г. Рорером и Э. Руска.

В туннельном микроскопе вдоль исследуемой поверхности перемещается зонд - тонкая игла. Игла сканирует исследуемую поверхность, находясь так близко от нее, что электроны из электронных оболочек (электронных облаков) поверхностных атомов за счет волновых свойств могут попасть на иглу. Для этого на иглу подаем “плюс” от источника, а на исследуемый образец - “минус”. Туннельный ток пропорционален коэффициенту прозрачности потенциального барьера между иглой и поверхностью, который согласно формуле (1.7.16) зависит от ширины барьера l. При сканировании иглой поверхности образца туннельный ток изменяется в зависимости от расстояния l, повторяя профиль поверхности. Прецизионные перемещения иглы на малые расстояния осуществляют с помощью пьезоэффекта, для этого закрепляют иглу на кварцевой пластине, которая расширяется или сжимается, когда к ней прикладывается электрическое напряжение. Современные технологии позволяют изготовить иглу столь тонкую, что на ее конце располагается один единственный атом.

Изображение формируется на экране дисплея ЭВМ. Разрешение туннельного микроскопа так высоко, что позволяет “увидеть” расположение отдельных атомов. На рис.1.10 приведено в качестве примера изображение атомной поверхности кремния.

2. Альфа-радиоактивность (a– распад ). В этом явлении происходит спонтанное превращение радиоактивных ядер, в результате которого одно ядро (его называют материнским) испускает a – частицу и превращается в новое (дочернее) ядро с зарядом, меньшим на 2 единицы. Напомним, что a – частица (ядро атома гелия) состоит из двух протонов и двух нейтронов.

Если считать, что a- частица существует как единое образование внутри ядра, то график зависимости ее потенциальной энергии от координаты в поле радиоактивного ядра имеет вид, показанный на рис.1.11. Он определяется энергией сильного (ядерного) взаимодействия, обусловленного притяжением нуклонов друг к другу, и энергией кулоновского взаимодействия (электростатического отталкивания протонов).

В результате a - частица в ядре, имеющая энергию Е_a, находится за потенциальным барьером. Вследствие ее волновых свойств есть некоторая вероятность того, что a- частица окажется за пределами ядра.

3. Туннельный эффект в p-n - переходе используется в двух классах полупроводниковых приборов: туннельных и обращенных диодах. Особенностью туннельных диодов является наличие падающего участка на прямой ветви вольт-амперной характеристики - участка с отрицательным дифференциальным сопротивлением. В обращенных диодах наиболее интересным является то, что при обратном включении сопротивление оказывается меньше, чем при обратном включении. Подробнее о туннельных и обращенных диодах см. раздел 5.6.