Одномерной прямоугольной потенциальной яме
Рассмотрим микроскопическую частицу, движение которой ограничено вдоль оси x непроницаемыми для нее стенками при x=0 и при x=l.
Потенциальная энергия частицы 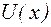 может быть представлена в этом случае в следующем виде:
может быть представлена в этом случае в следующем виде:
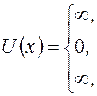
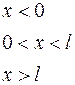 (1.6.1)
(1.6.1)
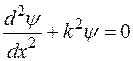 . (1.6.7)
. (1.6.7)
Решение дифференциального уравнения (1.6.7) будем искать в виде
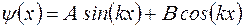 . (1.6.8)
. (1.6.8)
Волновые функции 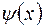 должны удовлетворять граничным условиям (1.6.4) и (1.6.5). Подставим выражение (1.6.8) в граничное условие (1.6.4), получим
должны удовлетворять граничным условиям (1.6.4) и (1.6.5). Подставим выражение (1.6.8) в граничное условие (1.6.4), получим
 ,
,
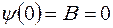 . (1.6.9)
. (1.6.9)
Отсюда
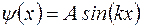 . (1.6.10)
. (1.6.10)
Подставим выражение (1.6.10) в граничное условие (1.6.5)
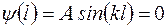 . (1.6.11)
. (1.6.11)
Условие (1.6.11) выполняется, если аргумент синуса равен
 , (1.6.12)
, (1.6.12)
где параметр n может принимать целочисленные значения: n= 1,2,3…
Из условия (1.6.12) следует, что волновое число k может принимать только дискретные значения
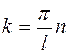 . (1.6.13)
. (1.6.13)
Дискретным значениям волнового числа соответствуют дискретные значения энергии
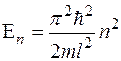 . (1.6.14)
. (1.6.14)
Из выражения (1.6.14) следует, что энергия частицы в потенциальной яме не может быть произвольной. Она принимает определенные дискретные значения.
Значения энергии 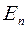 называются собственными значениями. Соответствующие этим значениям волновые функции называются собственными функциями. Собственными функциями для частицы в потенциальной яме будут
называются собственными значениями. Соответствующие этим значениям волновые функции называются собственными функциями. Собственными функциями для частицы в потенциальной яме будут
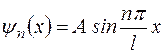 . (1.6.15)
. (1.6.15)
Коэффициент А может быть найден из условия нормировки волновой функции (1.3.4). Запишем это условие применительно к данной задаче
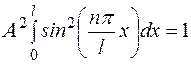 . (1.6.16)
. (1.6.16)
Для интегрирования выражения (1.6.16) и нахождения коэффициента A можно воспользоваться соотношением  . Расчет приводит к следующей формуле для нормировочного множителя
. Расчет приводит к следующей формуле для нормировочного множителя
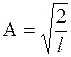 . (1.6.17)
. (1.6.17)
Окончательно получим
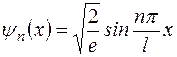 . (1.6.18)
. (1.6.18)
Плотность вероятности обнаружения частицы в различных точках ямы равна
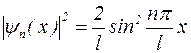 . (1.6.19 )
. (1.6.19 )
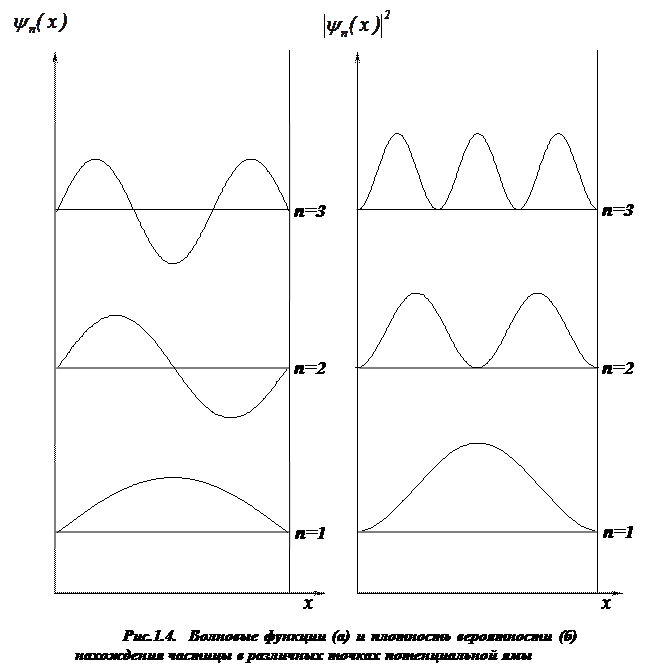 На рис.1.4. приведены волновые функции и распределение плотности вероятности обнаружения частицы вдоль координаты x для различных n.
На рис.1.4. приведены волновые функции и распределение плотности вероятности обнаружения частицы вдоль координаты x для различных n.
Из формулы (1.6.19) и рис.1.4 следует, чтовероятность обнаружения частицы в различных местах ямы неодинакова. Необходимо отметить, что такое поведение частицы несовместимо с представлениями о траекториях.
Используя формулу (1.6.13) и соотношение между длиной волны и волновым числом 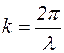 , можно рассчитать число длин волн де Бройля, укладывающихся на ширине потенциальной ямы. Получим
, можно рассчитать число длин волн де Бройля, укладывающихся на ширине потенциальной ямы. Получим
 ;
; 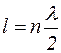 . (1.6.20)
. (1.6.20)
 Из выражения (1.6.20) следует, что на ширине ямы укладывается целое число длин полуволн, равное значению квантового числа n (рис.1.4)
Из выражения (1.6.20) следует, что на ширине ямы укладывается целое число длин полуволн, равное значению квантового числа n (рис.1.4)
Физические величины, которые могут принимать лишь определенные дискретные значения, называют квантованными. Квантованные значения энергии 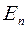 называют уровнями энергии, они образуют энергетический спектр частицы. Числа n, определяющие энергетические уровни, называют квантовыми числами.
называют уровнями энергии, они образуют энергетический спектр частицы. Числа n, определяющие энергетические уровни, называют квантовыми числами.
Определим энергетический интервал между двумя соседними уровнями энергии (рис.1.5). Он равен
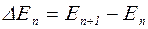 . (1.6.21)
. (1.6.21)
При достаточно больших n
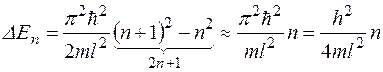 . (1.6.22)
. (1.6.22)
Исследуем влияние линейных размеров потенциальной ямы на квантование энергии частицы. Для этого проведем некоторые оценки. Рассмотрим движение электрона (его масса равна  кг).
кг).
1. Пусть размер ямы соизмерим с размерами атома, то есть 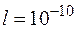 ¸
¸ 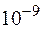 м. Тогда
м. Тогда
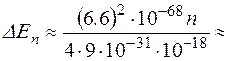
 Дж
Дж 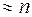 эВ
эВ
Сравним это значение с энергией теплового движения (величиной порядка kT), которая при комнатной температуре составляет примерно 0,025 эВ. В этом случае DEn >> kT, и дискретность энергетических уровней будет проявляться весьма заметно.
2. Пусть размер ямы велик, то есть 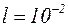 м (свободные электроны в металле). Тогда
м (свободные электроны в металле). Тогда
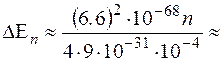
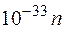 Дж
Дж 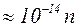 эВ.
эВ.
Получили DEn << kT . Энергетические уровни расположены очень густо, и энергетический спектр можно считать квазинепрерывным.
Найдем отношение энергетического интервала 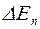 между уровнями к соответствующему значению энергии
между уровнями к соответствующему значению энергии 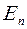 . Оно будет равно
. Оно будет равно
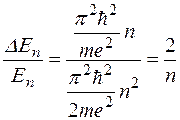 (1.6.23)
(1.6.23)
При увеличении квантового числа n отношение 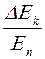 уменьшается. Происходит относительное сближение энергетических уровней частицы в потенциальной яме. Если n велико (n>>1), то энергетический спектр можно считать квазинепрерывным.
уменьшается. Происходит относительное сближение энергетических уровней частицы в потенциальной яме. Если n велико (n>>1), то энергетический спектр можно считать квазинепрерывным.
Данный результат является частным случаем принципа соответствия Бора, согласно которому выводы и результаты квантовой механики при больших квантовых числах должны соответствовать классическим результатам.
Дата добавления: 2015-11-10; просмотров: 1304;
