Состояния электрона в атоме водорода

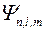
Уровень энергии	Волновая функция	Значение	Число состояний
n	l	m
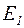
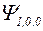
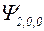
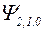
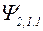
			+1
			-1
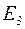
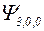
					Всего
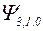
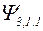
			+1
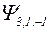
			-1
--------	------	------	------

1.9. 1s– состояние электрона в атоме водорода

Волновая функция электрона для 1s – состояния зависит только от расстояния r электрона от ядра, т.е. является сферически симметричной. Ее выражение имеет вид

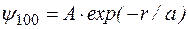. (1.9.1)

Здесь 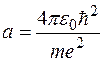и совпадает с формулой радиуса первой боровской орбиты; численное значение этого параметра равно ; A – множитель, который можно определить из условия нормировки волновой функции

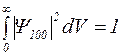(1.9.2)

Исходя из сферической симметрии задачи, выберем элемент объема 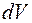в виде тонкого сферического слоя радиуса r толщиной dr (рис.1.14).

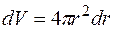(1.9.3)

Подставим выражения (1.9.1) и (1.9.2) в условие нормировки (1.9.3), получим

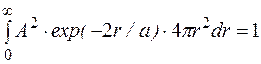
или 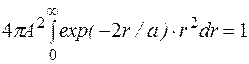. (1.9.4)

Интеграл в выражении (1.9.4) можно взять по частям. Он будет равен

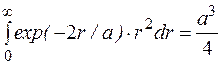. (1.9.5)

Для нормировочного множителя получим выражение

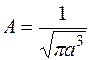. (1.9.6)

Окончательно, нормированная волновая функция электрона в 1s – состоянии имеет вид

(1.9.7)

Вероятность обнаружить электрон в элементе объем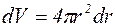а равна

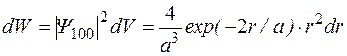(1.9.8)

Найдем наиболее вероятное расстояние электрона от ядра. Для этого введем функцию

. (1.9.9)

Функция 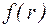определяет плотность вероятности обнаружения электрона на расстоянии r от ядра. 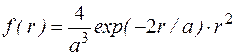. (1.9.10)

График этой функции представлен на рис.1.15.

Наиболее вероятное расстояние электрона от ядра соответствует максимуму функции 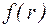. Для нахождения положения максимума необходимо приравнять нулю производную 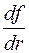, или

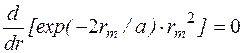. (1.9.11)

Расчет приводит к результату

r_m=a . (1.9.12)

Таким образом, наиболее вероятное расстояние электрона от ядра равно радиусу первой боровской орбиты.