Атом водорода в квантовой механике.

Квантовые числа

Атом – наименьшая частица вещества, обладающая всеми химическими свойствами элемента. Простейшим атомом является атом водорода, состоящий из одного протона и одного электрона.

Рассмотрим движение электрона в кулоновском поле ядра с зарядом 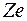. При Z=1 такая система соответствует атому водорода, при иных Z – водородоподобному иону. Водородоподобными ионами принято называть ионы 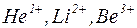, имеющие ядро с зарядом 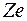и один электрон.

Потенциальная энергия электрона зависит от его расстояния от ядра и определится формулой

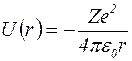. (1.8.1)

Эта зависимость представлена графически на рис.1.12. Поэтому принято говорить, что электрон в водородоподобном атоме находится внутри гиперболической центрально-симметричной потенциальной ямы.

Запишем уравнение Шредингера для этого случая

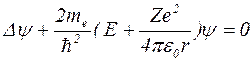. (1.8.2)

Здесь 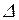- оператор Лапласа. Так как потенциальная яма имеет центрально- симметричную форму, то оператор Лапласа необходимо взять в сферической системе координат: 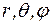и волновые функции в общем случае будут зависеть от координат 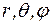. Данная задача успешно решена в квантовой механике, но решение ее достаточно громоздкое, и мы его здесь не приводим. Рассмотрим лишь основные результаты, которые следуют из решения уравнения (1.8.2).

Уравнение (1.8.2 ) имеет решение в следующих случаях:

§ при любых положительных значениях энергии электрона E>0. Этот случай соответствует свободному электрону, не связанному с атомом;

§ при дискретных отрицательных значениях энергии

, (n = 1, 2, 3….). (1.8.3)

Значения 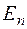называют собственными значениями.

Собственные функции уравнения содержат 3 целочисленных параметра. Их называют квантовыми числами и обозначают n, l, m.

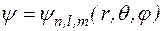. (1.8.4)

Параметр n называется главным квантовым числом. Оно определяет энергию электрона в атоме и может принимать любые целочисленные значения. Энергия электрона в атоме квантуется.

Число l называется орбитальным квантовым числом. При данном n оно может принимать значения: l =0, 1, 2…. , n -1 (всего n значений).

Орбитальное квантовое число l определяет возможные значения момента импульса электрона L

. (1.8.5)

Момент импульса электрона квантуется.

Различные значения орбитального квантового числа электрона служат для систематики электронных состояний в атомах и молекулах. Приняты следующие обозначения:

l=0 – s –состояние;

l =1 – p –состояние;

l =2 – d –состояние;

l =3 – f –состояние.

Значение главного квантового числа указывается перед условным обозначением квантового числа l. Возможны следующие состояния электрона:

1s,

2s, 2p,

3s, 3p, 3d,

4s, 4p, 4d, 4f и т.д.

Число m называется магнитным квантовым числом. При заданном l магнитное квантовое число может принимать значения:

m_l=0, ±1, ±2, ….,±l, (всего 2l +1 значение).

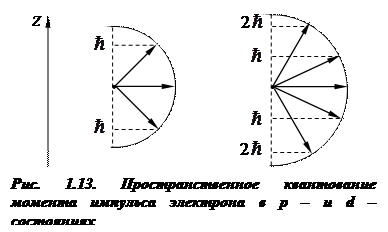
Магнитное квантовое число определяет возможные значения проекции орбитального момента импульса на направление внешнего магнитного поля. Это означает, что существует пространственное квантование: вектор момента импульса 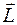может иметь только вполне определенные дискретные ориентации в пространстве. Проекция момента импульса на направление Z может принимать значения

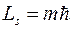(1.8.6)

На рис.1.13 показано пространственное квантование вектора 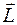для электронов в p– и d– состояниях.

Различные состояния атома с одинаковой энергией называются вырожденными, а число состояний с одинаковой энергией называется кратностью вырождения. Число различных состояний соответствующих данному n и различным l и m можно рассчитать по формуле

. (1.8.7)

Таким образом, каждый уровень энергии атома водорода имеет вырождение кратности n². В таблице 1.2 приведены состояния, соответствующие первым трем энергетическим уровням.

Таблица 1.2.