Спин электрона. Принцип Паули

В настоящее время доказано, что кроме орбитального механического момента электрон обладает собственным моментом импульса. Собственный момент импульса называется спином. Собственный момент импульса электрона был обнаружен в опытах Штерна и Герлаха.

Целью опытов являлось измерение магнитных моментов атомов. Сущность опыта заключалась в следующем. Узкий пучок атомов пропускался через неоднородное магнитное поле. Для атомов с одним валентным электроном в s – состоянии собственный орбитальный механический и магнитный моменты раны нулю, следовательно, такой пучок атомов не должен испытывать отклонения в неоднородном магнитном поле. Но в опытах наблюдалось расщепление пучка на два, обусловленное пространственным квантованием спинового магнитного момента.

Спиновый момент импульса электрона определяется формулой

. (1.10.1)

Здесь s–спиновое квантовое число. Спиновое квантовое число имеет только одно значение

. (1.10.2)

Проекция спина на направление внешнего магнитного поля может принимать значения

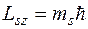, (1.10.3)

где - магнитное спиновое число. Так как существует всего 2 ориентации спинового момента на направление внешнего поля, то m_S = ±1/2.

В связи с существованием спина электрона к квантовым числам n, l, m нужно добавить еще и квантовое число m_S. Таким образом, состояние каждого электрона в атоме характеризуется набором четырех квантовых чисел:

§ главным квантовым числом n (n=1,2,3………);

§ орбитальным квантовым числом l (l =0,1,2…….n-1);

§ магнитным квантовым числом m (m =0, ±1,… ±l);

§ магнитным спиновым квантовым числом m_S (m_S = ±1/2) .

В 1925 г. Паули установил квантовомеханический закон, называемый принципом Паули или принципом исключения.

Простейшая формулировка принципа Паули заключается в следующем.

В любой системе, содержащей множество электронов, не может быть более одного электрона с одинаковым набором четырех квантовых чисел n, l, m, m_S:

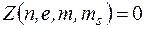или 1 .

Принцип Паули справедлив для всех частиц, для которых . Эти частицы называют фермионами.