Уравнение Шредингера. Основным уравнением нерелятивистской квантовой механики является уравнение Шредингера (1926 г.)

Основным уравнением нерелятивистской квантовой механики является уравнение Шредингера (1926 г.). Это уравнение не выводится из каких-либо известных ранее соотношений, а является исходным основным предположением; справедливость его доказывается согласием с опытом получаемых с его помощью результатов.

Запишем его

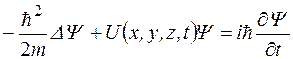. (1.4.1)

Здесь 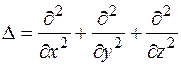– дифференциальный оператор Лапласа; 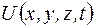– потенциальная энергия частицы в силовом поле, m – ее масса; 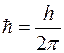; 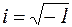– мнимая единица.

Уравнение Шредингера дополняется условиями, которые накладываются на волновую функцию :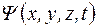

§ волновая функция должна быть конечной, однородной, непрерывной;

§ производные 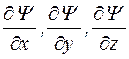должны быть непрерывны;

§ интеграл 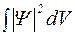должен быть конечным.

Эти условия называют стандартными условиями.

Уравнение (1.4.1) называется общим (временным) уравнением Шредингера. Во многих задачах квантовой механики силовое поле, в котором движется частица, стационарно. Это означает, что ее потенциальная энергия не зависит от времени и является функцией только координат, т.е. .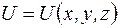

В этом случае волновую функцию 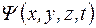можно представить в виде двух сомножителей

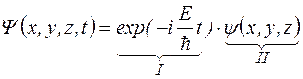(1.4.2 )

В этом выражении E – полная энергия частицы. Первый сомножитель 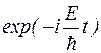зависит только от времени и называется временной частью волновой функции. Второй сомножитель 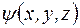зависит только от координат и называется координатной частью волновой функции.

Подставим соотношение (1.4.2) в уравнение Шредингера (1.4.1), получим

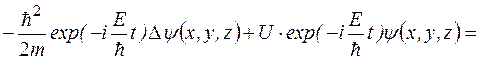
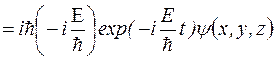. (1.4.3)

Сокращая выражение (1.4.3) на 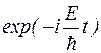и преобразуя, получим

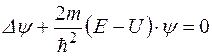. (1.4.4)

Уравнение (1.4.4) называется уравнением Шредингера для стационарных состояний.