Соотношение неопределенностей
С точки зрения классической физики всякая частица в любой момент времени имеет вполне определенную координату и обладает определенным импульсом. Иными словами, возможность одновременного точного определения координаты и импульса частицы является характерным свойством классических частиц. Волновые свойства микрочастиц вносят ограничения в применение к ним таких понятий как координата, импульс, траектория. Действительно, такое понятие как «длина волны в данной точке» лишено физического смысла, поскольку волновой процесс не может быть локализован в определенной точке пространства.
Учитывая волновые свойства микрочастиц, Вернер Гейзенберг (1927) установил соотношения, называемые соотношениями неопределенностей.
Соотношениями неопределенностей называются неравенства:
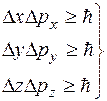 (1.2.1)
(1.2.1)
Здесь  – интервалы координат, в которых может быть локализована частица;
– интервалы координат, в которых может быть локализована частица; 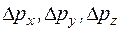 – интервалы координат, в которых заключены проекции импульса частицы;
– интервалы координат, в которых заключены проекции импульса частицы; 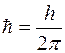 .
.
Соотношения Гейзенберга показывают, что координаты частиц x, y, z и проекции ее импульса 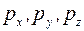 не могут одновременно иметь значения, в точности равные
не могут одновременно иметь значения, в точности равные 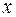 и
и 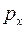 ,
, 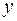 и
и 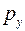 ,
, 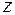 и
и 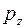 . Чем более точно определено положение частицы (т.е. чем меньше
. Чем более точно определено положение частицы (т.е. чем меньше 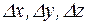 ), тем менее точно определена проекция ее импульса (т.е. тем больше
), тем менее точно определена проекция ее импульса (т.е. тем больше 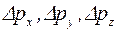 ). Если положение частицы на оси
). Если положение частицы на оси 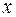 определено точно (
определено точно ( 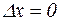 ), то неопределенность ее импульса стремится к бесконечности (
), то неопределенность ее импульса стремится к бесконечности ( 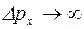 ), значение
), значение 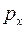 становится совершенно неопределенным.
становится совершенно неопределенным.
Необходимо отметить, что невозможность точного одновременного определения координаты и импульса не связана с несовершенством методов измерения или измерительных приборов. Она является следствием специфики микрообъектов, их объективных свойств.
Рассмотрим несколько примеров.
Пример 1. Необходимо выяснить, применимо ли понятие траектории к движению электрона в электронно-лучевой трубке. Исходные данные:
cкорость электронов v = 10 7 м/c и определена с точностью до 0.01%;
размер пятна на экране 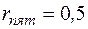 мм
мм 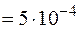 м;
м;
масса электрона 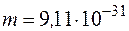 кг.
кг.
Неопределенность скорости Dv будет равна
Dv  м/с
м/с
Неопределенность координаты 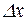
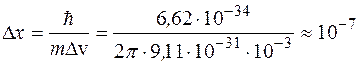 м.
м.
Из сравнения величин 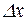 и
и 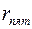 следует, что неопределенность координаты много меньше размера пятна на экране, поэтому в данном случае можно говорить о движении электронов по определенной траектории.
следует, что неопределенность координаты много меньше размера пятна на экране, поэтому в данном случае можно говорить о движении электронов по определенной траектории.
Пример 2. Необходимо выяснить, применимо ли понятие траектории к движению электрона в атоме водорода. Исходные данные:
размеры атома составляют величину 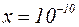 м; скорость электрона, рассчитанная из классических представлений, равна
м; скорость электрона, рассчитанная из классических представлений, равна 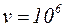 м/с.
м/с.
Найдем неопределенность значения скорости
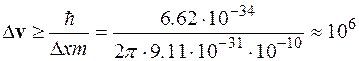 м/с.
м/с.
Величина неопределенности скорости Dv имеет такой же порядок, как и сама скорость. v Траектория электрона в атоме не имеет классического смысла.
Из рассмотренных примеров можно сделать следующие выводы.
Соотношение неопределенности являются квантовым ограничением применимости классической физики к микрообъектам. Для макроскопических тел они практически не вносят ограничений в возможность использования классических понятий координат и импульса.
Существует также соотношение неопределенностей для энергии и времени
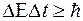 . (1.2.3)
. (1.2.3)
Соотношение (1.2.3) означает: система, имеющая конечное время жизни 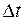 , не может быть охарактеризована определенным значением энергии. Неопределенность энергии
, не может быть охарактеризована определенным значением энергии. Неопределенность энергии 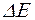 возрастает с уменьшением времени
возрастает с уменьшением времени 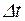 .
.
Рассмотрим излучение фотона атомом.
Неопределенность частоты излучения оценим, исходя из выражения для энергии фотона
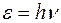 , (1.2.4)
, (1.2.4)
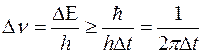 . (1.2.5)
. (1.2.5)
Здесь 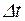 – время излучения.
– время излучения.
Из выражения (1.2.5) следует, что спектральные линии размыты, они имеют конечную ширину 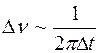 .
.
Из ширины спектральной линии можно оценить время жизни атома в возбужденном состоянии.
Волновая функция
Наличие у микрочастиц волновых свойств означает, что микрочастице следует сопоставить некоторое волновое поле. Амплитуда этого волнового поля зависит от координат и времени и называется волновой функцией. Волновую функцию принято обозначать с помощью символа 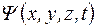 или (в кратком варианте) просто
или (в кратком варианте) просто 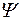 .
.
Физическое толкование волновой функции было дано Максом Борном. Оно заключается в следующем.
Рассмотрим элемент объема пространства 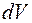 . Вероятность обнаружения частицы в объеме
. Вероятность обнаружения частицы в объеме 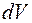 в момент времени
в момент времени 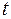 будет равна
будет равна
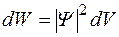 . (1.3.1)
. (1.3.1)
Здесь 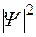 - квадрат модуля волновой функции.1
- квадрат модуля волновой функции.1
Необходимо отметить, что сама волновая функция не имеет физического смысла, смысл имеет квадрат ее модуля 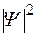 . Из формулы (1.3.1) следует, что
. Из формулы (1.3.1) следует, что
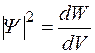 . (1.3.2)
. (1.3.2)
Таким образом, квадрат модуля волновой функции есть плотность вероятности обнаружения частицы в данной точке пространства.
Вероятность нахождения частицы в ограниченной области внутри некоторого объема 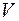 определится интегралом, взятым по этому объему
определится интегралом, взятым по этому объему
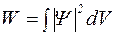 . (1.3.3)
. (1.3.3)
Возьмем этот интеграл по всему пространству. Так как пребывание частицы в какой-нибудь (любой) точке пространства есть событие достоверное, то интеграл по всему пространству (в бесконечных пределах) должен быть равен 1.
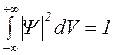 (1.3.4)
(1.3.4)
Условие (1.3.4) называется условием нормировки волновой функции.
Если волновая функция известна, то средние значения физических величин, характеризующих данный микрообъект, могут быть найдены по формуле
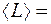
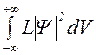 . (1.3.5)
. (1.3.5)
Здесь 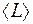 - среднее значение величины. Интегрирование производится по всей области пространства.
- среднее значение величины. Интегрирование производится по всей области пространства.
Дата добавления: 2015-11-10; просмотров: 1460;
