Интегрирование уравнения (20.11) даёт следующее соотношение

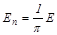, ( 20.11 )

то есть излучательная способность в направлении нормали в π раз меньше полной лучеиспускательной способности тела. Опыт показывает, что закон Ламберта строго справедлив только для абсолютно чёрного тела, а у серых тел он достаточно точно подтверждается лишь в пределах от 0 до 60°.

Связь между излучательной способностью и поглощательной способностью тел определяет закон Киргофа, который гласит, что отношение этих эффектов одинаково для всех серых тел, находящихся при одной температуре, и равно излучательной способности абсолютно черного тела при той же температуре:

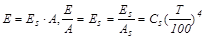. (20.13)

Из закона Киргофа следует, что степень черноты серого тела численно равна коэффициенту поглощения:

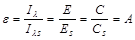(20.14)

20.2 Лучистый теплообмен между параллельными

пластинами

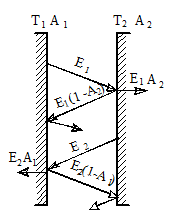
Пусть теплообмен происходит в прозрачной среде, а сами пластины будут непрозрачными и, имея температуры 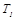, , 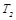коэффициенты поглощения 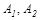, обладают энергией собственного излучения 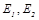(рисунок 20.3).

Полное эффективное излучение первого тела, складывающееся из собственного Е₁ и отраженного (с учетом поглощения) излучения второго тела:

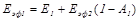(20.15)

Полное эффективное излучение второго тела составляет

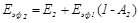(20.16)

Результирующая плотность теплового потока равна

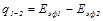(20.17)

Из совместного решения уравнений (20.15-20.16) следует

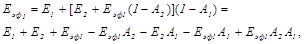
откуда

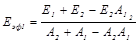(20.18)

Аналогично определяется полное эффективное излучение второго тела 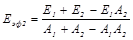(20.19)

После подстановки значений эффективных излучений тел в формулу (20.17) плотность теплового потока составляет

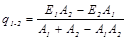(20.20)

В соответствии с законом Стефана-Больцмана собственная энергия излучения взаимодействующих тел равна

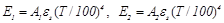
C учетом последних выражений

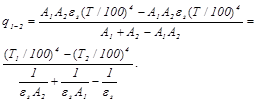
Окончательно

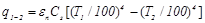( 20.21)

где 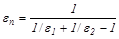- приведённая степень черноты

20.3 Использование экранов для защиты от теплового излучения

Для защиты от перегрева отдельных элементов теплотехнического оборудования или для уменьшения тепловых потерь иногда требуется уменьшить лучистый теплообмен. В этом случае между излучающим и нагреваемым элементами устанавливают тонкие перегородки или оболочки, называемые экранами.

Схема передачи лучистой энергии в системе двух плоскопараллельных поверхностей с расположенным между ними экраном показана на рисунке 20.4.

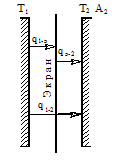В стационарном режиме теплообмена вся поглощаемая экраном энергия от излучаемого тела 1 будет излучаться им на второе тело 11, но часть падающего на экран лучистого потока будет отражаться им в сторону первого тела и принять, что степени черноты обоих тел и экрана равны ( 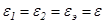), температура первого тела Т₁ больше температуры второго тела Т₂, а термическое сопротивление теплопроводности тонкостенного экрана равно нулю и температуры на обеих его поверхностях одинаковы, то приведенные степени черноты систем “первое тело - экран” и “второе тело - экран” будут равными

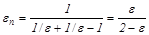(20.22)

От горячей пластины к экрану передается лучистый поток

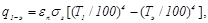(20.23)

а от экрана к более холодной поверхности

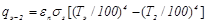(20.24)

В стационарном режиме эти лучистые потоки равны:

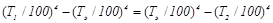(20.25)

Из формулы (20.25) следует

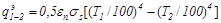(20.26)

Из сравнения формул (5.26) и (5.21) следует, что в случае применения экрана лучистый тепловой поток уменьшился вдвое.

При установке n экранов снижение теплоотдачи излучением по сравнению с безэкранной системой подчиняется выражению

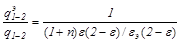, (20.27)

где 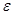- степень черноты теплопередающих поверхностей, 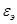- степень черноты экрана.

20.4 Теплообмен излучением между телами, одно из которых находится внутри другого

Примером такого теплообмена может быть лучистый теплообмен между горячей трубой и стенами обогреваемого помещения, в котором проложена труба. Сложность расчета в такой схеме (рисунок 20.5) связан с тем, что каждое из тел, участвующих в энергообмене излучает на другое лишь часть энергии, а остальная энергия рассеивается в пространстве.

Для учета этой особенности в расчетную формулу (20.21) вводится поправочный коэффициент облученности тела j, учитывающий долю излучения первого (малого) тела, которое воспринимается вторым (большим) телом:

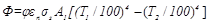(20.28)

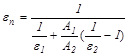где - приведенная степень черноты,

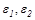- степени черноты, соответственно, первого и второго тел,

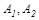- площади первого и второго тел.

Коэффициент облучённости есть чисто геометрический фактор, зависящий от формы, размеров и взаимного расположения тел.

Если поверхность первого тела мала по сравнению с поверхностью второго тела 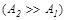, то расчет ведётся по следующей формуле:

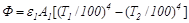
(20.29)

20.5 Излучение в поглощающей среде

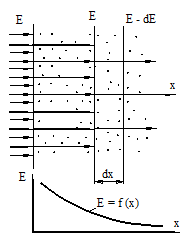
Примером поглощающей и излучающей среды могут быть продукты сгорания твердого топлива, содержащие зольный остаток и сажу. Пусть тепловой луч направлен вдоль оси х (рисунок 20.6) и входит в рассматриваемую запыленную зону площадью 1 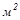с начальной энергией .

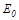Для упрощения частицы пыли будут рассматриваться как абсолютно чёрные сферы одинакового размера с диаметром d. В слое толщиной dx частицы, встретившиеся на пути луча, поглощают энергию dE, которая равна произведению энергии Е на суммарную площадь поперечного сечения всех частиц в слое dx. Воспринимающая лучистую энергию площадь частиц равна площади одной частицы на их число.

Число частиц в единице объема 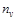равно отношению их массы в единице объема 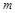к массе одной частицы 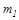, которая равна

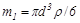, (20.30)

где r - плотность вещества, из которого состоят частицы.

Число частиц в объеме слоя толщиной dx и площадью 1 м составляет

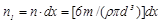(20.31)

Поглощенная в слое энергия

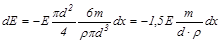(20.32)

Из последнего выражения следует

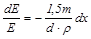(20.33)

После интегрирования в пределах изменения энергии от начального до текущего значения получается

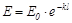, (20.34)

где l - толщина запыленного слоя, 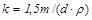- коэффициент ослабления лучистого потока.

Последнее выражение (20.34) отражает закон Бугера, который гласит: коэффициент ослабления излучения увеличивается с ростом массовой концентрации частиц и уменьшением их размеров.

В отличие от твердых тел коэффициент поглощения и степень черноты запыленной среды зависит не от поверхностных факторов, а от олщины и концентрации частиц.

Процесс распространения лучистой энергии в многоатомных газах имеет много общего с рассмотренным случаем. Роль частиц, поглощающих энергию, в этих газах играют молекулы.

20.6 Излучение газов

Излучение газов значительно отличается от излучения твердых тел. Одноатомные и двухатомные газы обладают ничтожно малой излучательной и поглощательной способностью, они практически прозрачны для тепловых лучей. Трехатомные ( 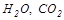и др.), а также многоатомные газы испускают тепловые лучи и поглощают их, поэтому в расчетах, связанных с горением углеводородных топлив, следует учитывать эти особенности. Механизм излучения и поглощения в этих газах похож на то, что происходит в запыленной среде, описанный в предыдущем параграфе.

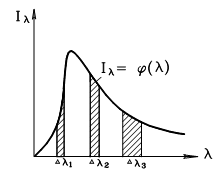Так как спектры излучения газов носят избирательный характер, то они поглощают и излучают энергию только в определенных интервалах длин волн, как это показано на рисунке 20.7, а для лучей с другими длинами волн они прозрачны. Расчет теплообмена излучением между стенками и газом достаточно сложен и для конкретных случаев дан в специальной литературе .

Наиболее простой метод расчета лучистого теплообмена между газом и стенкой базируется на уравнении Стефана-Больцмана:

,

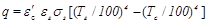где 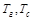- температуры газа и стенки, 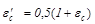- эффективная степень черноты стенки, 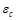- степень черноты стенки, 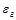- степень черноты газа.

Введение эффективной степени черноты стенки вызвано влиянием на степень черноты стенки излучающего газа. При 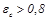используется выражение

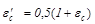
Степень черноты газа определяется в зависимости от температуры по специальным номограммам [2,5] с учетом парциального давления излучающего газа (водяных паров или углекислого газа) и средней длины пути луча

,

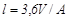где V - объем излучающего газа, А - площадь оболочки, в которой находится газ. Если газ содержит и водяной пар, и углекислоту, то степень черноты такой смеси определяется по формуле

,

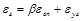где степени черноты водяных паров 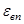и углекислого газа 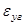, а также поправочный коэффициент поправочный коэффициент b определяются по графикам.