Основні теореми подвійності

Основним теоретичним результатом лінійного програмування є теореми подвійності, інтерпретація яких у термінах різних економічних завдань виявляється ефективним засобом економічного аналізу, спрямованим на найкраще використання ресурсів.

Перша теорема подвійності:

Для двох взаємно двоїстих ЗЛП має місце один з взаємовиключних випадків:

1. Якщо одна із задач двоїстої пари має рішення, то й інша вирішувана. При цьому оптимальні значення цільових функцій обох завдань збігаються:

. (7)

2. Якщо в одній із задач цільова функція на допустимій безлічі не обмежена зверху, то допустима безліч другого завдання порожня (тобто друга задача взагалі не має рішення).

3. Області визначення обох завдань є порожні множини.

Друга теорема подвійності (теорема рівноваги):

Для того, щоб X = (x₁,x₂, ..., х_п) і Y =(у₁,у₂, …, у_m) – припустимі рішення відповідно вихідної та двоїстої задач – були їх оптимальними рішеннями, необхідно і достатньо виконання таких умов «доповнюючої не жорсткості»:

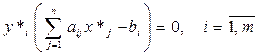, (8)

. (9)

Іншими словами, допустимі плани Х і Y пари двоїстих задач оптимальні тоді і тільки тоді, коли вони задовольняють таким умовам:

1) якщо x_j > 0, то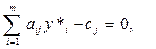

2) якщо y_i > 0, то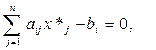

3) якщо то x_j = 0,

4) якщо 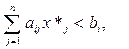то y_i = 0.

Умови (8)-(9) дозволяють по оптимальному рішенню однієї з взаємно двоїстих задач, знайти оптимальне рішення іншої задачі. Тому для розв’язання певної ЗЛП можна спочатку розв’язати двоїсту задачу, а потім визначити рішення вихідної задачі.

Третя теорема подвійності (теорема про оцінки):

Значення змінних у_i в оптимальному рішенні двоїстої задачі являють собою оцінки впливу вільних членів b_i системи обмежень (нерівностей) прямої задачі на величину цільової функції вихідної задачі, вони рівні:

. (10)

Звідси випливає, що приріст цільової функції DF визначається добутком приросту запасу ресурсів Db_i на величину оптимальної оцінки у_i. Рівність справедлива, якщо величина Db_i є відносно невеликою (межі зміни встановлюються на основі теорії стійкості оптимальних рішень ЛП).

Розглянемо економічну інтерпретацію теорем подвійності і сформулюємо властивості оптимальних оцінок, що випливають з цих теорем.