Формулювання двоїстої задачі лінійного програмування, її економічна інтерпретація
Якщо деяку економічну проблему зведено до розгляду задачі математичного програмування, то її рішення містить два істотно різних набори економічних величин. В один з них (так зване «пряме рішення») входять всі об'ємні та структурні показники, що характеризують випуск продукції і використання виробничих ресурсів. Інший набір («двоїсте рішення») складається з величин, що характеризують вплив можливих збільшень кожного продукту і ресурсу на досягнення мети рішення задачі. Ці величини називаються оцінками оптимального плану (подвійними оцінками). Вони являють собою важливий засіб економіко-математичного аналізу господарських рішень.
Оцінки дозволяють визначати напрям зміни оптимального плану у разі зміни початкових умов (обмежень). При не надто великому варіюванні цих умов оцінки дають можливість безпосередньо судити про нову величину критерію оптимальності (величину цільової функції), дозволяючи тим самим досліджувати стійкість оптимуму по відношенню до змін початкових умов і полегшуючи вірне рішення низки економічних питань, від яких залежать вихідні передумови розглянутої задачі.
Значна роль оптимальних оцінок і при визначенні доцільності застосування нових способів використання ресурсів, невідомих при початковій постановці завдання. На основі отриманих оптимальних оцінок визначають прибутковість або збитковість (з погляду поставленої мети) нового способу. І якщо останній виявляється прибутковим, то раніше складений оптимальний план вже не вважається оптимальним – застосування нового способу доцільно.
Розглянемо модель виробничої системи з погляду цінності наявних у підприємства ресурсів. Ресурси, які в оптимальному плані не використовуються повністю, не має сенсу нарощувати навіть при порівняно невеликих витратах на збільшення їх запасів, тому говорять, що вони мають для виробничої системи низьку цінність. Найбільшу цінність матимуть ті ресурси, які повністю витрачаються в оптимальному плані і тому обмежують випуск продукції, а, отже, і дохід; на збільшення запасу цих ресурсів підприємство згідно нести значні витрати. У зв'язку з цим можна вважати, що кожен вид ресурсу має певну «тіньову ціну», яка визначає цінність відповідного ресурсу для підприємства з погляду доходу від реалізації продукції, що випускається і залежить від наявного запасу цього ресурсу і потреби в ньому для випуску продукції. Оптимальному стану виробничої системи відповідає вектор оптимальних тіньових цін наявного запасу ресурсів. Оптимальні тіньові ціни називають об'єктивно зумовленими оцінками, або оптимальними двоїстими оцінками ресурсів.
Для визначення оптимальних двоїстих оцінок ресурсів (оптимальних оцінок) складається задача лінійного програмування, яка має назву двоїстої; первісна задача називається вихідною, або прямою. Змінні двоїстої задачі і є двоїстими оцінками, або тіньовими цінами.
Моделі вихідної (прямої) і двоїстої задач в загальному вигляді можуть бути записані таким чином:
| Вихідна (пряма) задача | Двоїста задача |
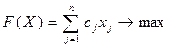 (1) (1)
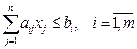 (2) (2)
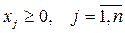 (3) (3)
| 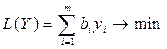 (4) (4)
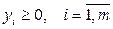 (5) (5)
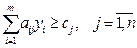 (6) (6)
|
Симетричні:
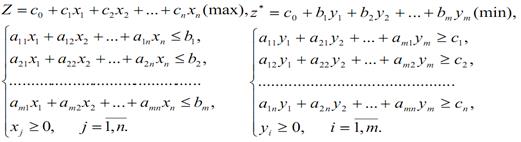
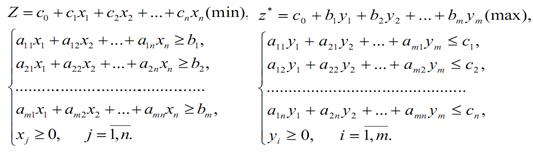
Несиметричні:
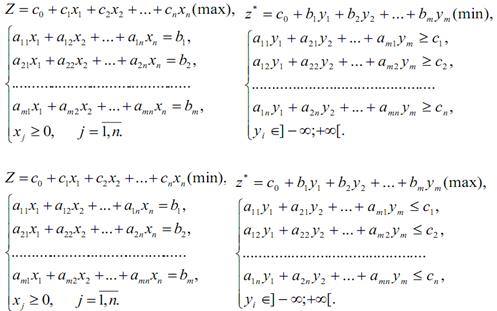
Виходячи з моделі розподілу ресурсів, пряме завдання відображає процес виробництва n видів продукції з використанням m видів ресурсів. Коефіцієнт цільової функції cj являє собою дохід (прибуток) на одиницю продукції j-го виду; коефіцієнти aij з обмежень задачі – це витрата ресурсів i-го виду на випуск одиниці j-ї продукції; права частина обмежень bi характеризує запас i-го ресурсу.
Ліва частина кожного обмеження (2) прямої задачі показує, скільки відповідного ресурсу необхідно на випуск продукції в кількості (х1, х2, ..., хn), а права – скільки ресурсу можна використовувати виходячи з наявного запасу.
Цільова функція виражає вимогу максимізації доходу від реалізації продукції в припущенні, що вся випущена продукція буде реалізованою.
Змінні двоїстої задачі уі представляють собою оцінку одиниці ресурсу i-го виду (сенс цих оцінок визначається їх властивостями, про які йтиметься далі). Величини уі мають бути такими, щоб сума тіньових цін ресурсів, що витрачаються на випуск одиниці будь-якого виду продукції, була не менша величини доходу cj:
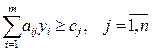 .
.
Отже, ліва частина обмеження двоїстої задачі (6) містить оцінку всіх ресурсів, що використовуються для виробництва одиниці продукції j-го виду, а права – прибуток від реалізації одиниці продукції j-го виду, тобто результат використання ресурсів.
Розмір цільової функції являє собою сумарну оцінку всіх наявних ресурсів:
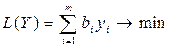 .
.
Економічна інтерпретація двоїстої задачі:
Припустимо, що з певних причин підприємство відмовляється від виробництва даної продукції і вирішує продати свої ресурси іншій організації. Виникає проблема встановлення об'єктивно обумовлених цін на ці ресурси. Якщо ціни позначити через уі, то цільова функція буде виражати інтереси фірми, що купує ресурси (найменша вартість ресурсів), а функціональні обмеження – інтереси підприємства. Підприємство не стане продавати ресурси, якщо прибуток від цього продажу буде менше прибутку від реалізації продукції, виробленої за допомогою цих ресурсів.
Пряма і двоїста задачі лінійного програмування тісно пов'язані між собою. Цей зв'язок полягає, в наступному:
1) якщо цільова функція вихідної задачі формулюється на максимум, то цільова функція двоїстої задачі – на мінімум і навпаки;
2) в задачі на максимум всі нерівності в функціональних обмеженнях мають вигляд (£), в задачі на мінімум – вид (³), і навпаки;
3) коефіцієнтами при невідомих у цільовій функції двоїстої задачі є вільні члени з системи обмежень вихідної задачі в стандартній формі;
4) правими частинами в обмеженнях двоїстої задачі служать коефіцієнти при невідомих із цільової функції вихідної задачі;
5) матриця А, складена з коефіцієнтів при невідомих в системі обмежень вихідної задачі, і аналогічна матриця АТ в двоїстій задачі виходять одна з одної транспонуванням;
6) число змінних в двоїстій задачі дорівнює числу функціональних обмежень вихідної задачі, а число обмежень у системі двоїстої задачі – числу змінних у вихідній;
7) кожному обмеженню однієї задачі відповідає змінна іншого завдання, номер змінної збігається з номером обмеження; знаки нерівностей в системі обмежень прямої задачі змінюються на протилежні в системі обмежень двоїстої задачі. При цьому обмеженню, записаному у вигляді нерівності, відповідає змінна, пов'язана умовою невід'ємності. Якщо функціональне обмеження вихідної задачі є рівністю, то відповідна змінна двоїстої задачі може приймати як позитивні, так і негативні значення.
Дві наведені задачі (1) - (3) і (4) - (6) утворюють пару симетричних двоїстих задач. Рішення однієї з них може бути отримано безпосередньо з рішення іншої.
Встановимо зв'язок між рішеннями прямої і двоїстої задач лінійного програмування.
Наведемо завдання до канонічного виду шляхом введення в ліву частину кожного обмеження додаткових змінних:
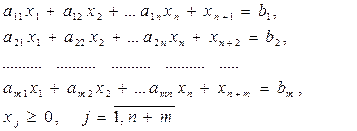
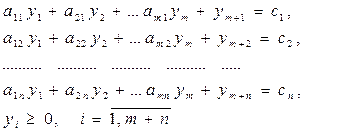
Кожна змінна xj (або yi) відповідає j-му (i-му) обмеженню в двоїстій для даній задачі, а отже, і додатковій змінній, введеної в це обмеження з метою перетворення його на рівність. Таким чином, встановлюється така відповідність між змінними:
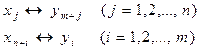 .
.
Говорять, що змінні прямої і двоїстої задач групуються у взаємозалежні пари 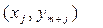 і
і 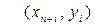 , що мають назву пари двоїстих змінних.
, що мають назву пари двоїстих змінних.
У двоїстій парі якщо одна змінна є базисною для одного із завдань, то відповідна їй інша змінна є вільною в двоїстому завданні. Економічний сенс додаткових змінних представимо у вигляді наступної таблиці (табл. 1).
Таблиця 1 – Економічний зміст додаткових змінних
| Задача | ліва частина обмеження | Права частина обмеження | Різниця |
| Вихідна | 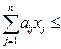 кількість необхідного ресурсу i-го виду
кількість необхідного ресурсу i-го виду
| 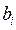 кількість наявного ресурсу i-го виду
кількість наявного ресурсу i-го виду
| 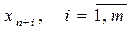 резерв ресурсу i-го виду (якщо ресурсу більше, ніж необхідно)
резерв ресурсу i-го виду (якщо ресурсу більше, ніж необхідно)
|
| Двоїста | 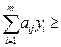 оцінка ресурсів, що витрачаються на випуск одиниці j-го продукту
оцінка ресурсів, що витрачаються на випуск одиниці j-го продукту
| 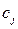 результат виготов-лення одиниці j-го продукту (витрат ресурсів)
результат виготов-лення одиниці j-го продукту (витрат ресурсів)
| 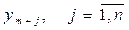 можливий збиток від виробництва одиниці j-го продукту (якщо витрати більше результату)
можливий збиток від виробництва одиниці j-го продукту (якщо витрати більше результату)
|
Дата добавления: 2015-11-10; просмотров: 2254;
