Постановка задач лінійного програмування і форми їх запису
При побудові економіко-математичної моделі лінійного програмування використовуються такі поняття:
1. Критерій оптимальності – це ознака, за якою безліч або одне рішення задачі визнається найкращим.
2. Цільова функція математично пов'язує між собою фактори моделі, її значення визначається значенням цих величин. Розуміння змісту цільової функції дає критерій оптимальності.
3. Система обмежень визначає межі існування області дійсних і допустимих рішень і характеризує основні зовнішні і внутрішні властивості об'єкта.
4. Рівняння зв'язку – це математична формалізація системи обмежень.
5. Рішення економіко-математичної моделі – набір значень змінних, які задовольняють її рівнянню зв'язку.
У загальному вигляді завдання лінійного програмування (ЗЛП) формулюється наступним так: потрібно знайти такі значення змінних 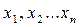 , при яких цільова функція
, при яких цільова функція
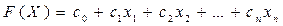 (3)
(3)
досягає максимуму (або мінімуму), і які задовольняють обмеженням:
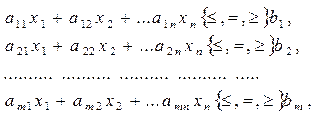 (4)
(4)
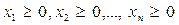 . (5)
. (5)
Функція (3) називається цільовою функцією, а система (4) - (5) – системою обмежень або системою умов задачі.
Будь-який набір змінних 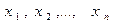 , який задовольняє всім обмеженням завдання, називається допустимим рішенням, або допустимим планом. Сукупність усіх допустимих планів називається допустимим безліччю, або областю допустимих рішень задачі. Допустиме рішення, яке звертає в максимум або мінімум цільову функцію, називається оптимальним рішенням, або оптимальним планом. Оптимальний план є рішенням задачі лінійного програмування.
, який задовольняє всім обмеженням завдання, називається допустимим рішенням, або допустимим планом. Сукупність усіх допустимих планів називається допустимим безліччю, або областю допустимих рішень задачі. Допустиме рішення, яке звертає в максимум або мінімум цільову функцію, називається оптимальним рішенням, або оптимальним планом. Оптимальний план є рішенням задачі лінійного програмування.
Залежно від наявності обмежень різного типу розрізняють наступні три основні форми ЗЛП.
Загальна задача лінійного програмування характеризується тим, що включає як обмеження-рівності, так і обмеження-нерівності, крім того, не на всі змінні накладається умова невід'ємності. ЗЛП записана в канонічній формі, якщо всі обмеження представлені у вигляді рівностей і на всі змінні накладається умова невід'ємності. Такою є модель (9) - (11).
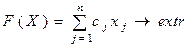 (9)
(9)
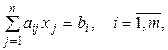 (10)
(10)
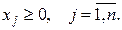 (11)
(11)
Симетрична форма задачі лінійного програмування містить тільки обмеження-нерівності і часто використовується в одному з наступних видів:
1. 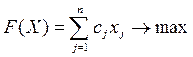 2.
2. 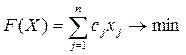
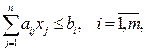
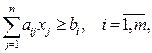
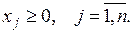
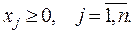
Перехід від однієї форми до іншої здійснюється на основі простих перетворень. Так, для переходу від обмеження-нерівності до рівності в ліву частину нерівності досить ввести додаткову невід’ємну змінну зі знаком (+), якщо нерівність типу «≤», і зі знаком (-), якщо нерівність типу «≥».
Від обмежень-рівностей можна перейти до нерівностей, замінюючи кожне рівняння
1. 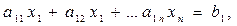
двома нерівностями протилежного типу:
2. 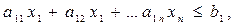
3. 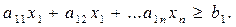
У багатьох випадках зручно розглядати інші форми запису ЗЛП. Так, канонічна задача в матричної формі запису має вигляд:
F(X) = CX → extr,
AX = B,
X ≥ 0,
де 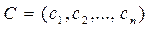 – вектор-рядок з коефіцієнтів при невідомих у цільовій функції;
– вектор-рядок з коефіцієнтів при невідомих у цільовій функції;
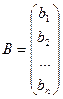 – вектор-стовпчик правих частин обмежень;
– вектор-стовпчик правих частин обмежень;
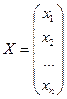 – вектор-стовпчик змінних задачі;
– вектор-стовпчик змінних задачі;
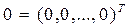 – нульовий вектор-стовпчик,
– нульовий вектор-стовпчик,
Т – знак транспонування;
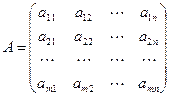 – матриця умов задачі.
– матриця умов задачі.
Часто використовують векторну форму запису ЗЛП:
F(X) = CX → extr,
A1 x1 + A2 x2 + … + An xn = B,
X ≥ 0,
де 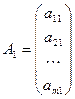 ,
, 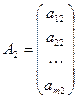 , … ,
, … , 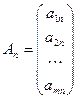 .
.
Дата добавления: 2015-11-10; просмотров: 2246;
