Тема 2. ОПТИМІЗАЦІЙНІ ЕКОНОМІКО-МАТЕМАТИЧНІ МОДЕЛІ

Розрізняють такі основні класи економіко-математичних моделей:

1. За ступенем агрегування об'єктів:

- макроекономічні моделі розглядають економіку як єдине ціле, пов'язуючи між собою укрупнені матеріальні та фінансові показники: ВВП, ВНП, споживання, інвестиції, зайнятість тощо. Ці моделі, абстрагуючись від поведінки окремих економічних елементів (домашні господарства і фірми), а також від відмінностей між окремими ринками, використовуються для аналізу і прогнозування цілісної економічної системи;

- мікроекономічні моделі описують поведінку основних структурних та функціональних елементів економічної системи і різні форми взаємодії цих елементів при заданих умовах.

2. За обліком фактора часу:

- статичні моделі описують деякий об'єкт у фіксований момент часу;

- динамічні моделі визначають взаємозв'язок змінних у часі.

3. Залежно від обліку фактора невизначеності:

- детерміновані моделі припускають жорсткі функціональні зв'язки між змінними моделі;

- стохастичні моделі допускають наявність випадкових впливів на досліджувані показники і використовують інструментарій теорії ймовірностей, математичної статистики, економетрії.

4. За характером математичного апарату:

- моделі лінійного та нелінійного програмування;

- кореляційно-регресійні моделі;

- моделі масового обслуговування;

- моделі мережного планування;

- моделі теорії ігор і т.д.

5. За призначенням:

- балансові (висловлюють вимоги відповідності наявності ресурсів і їх використання);

- трендові (розвиток економічної системи відбивається через тенденцію її основних показників);

- імітаційні (використовуються в процесі машинної імітації досліджуваних процесів або систем);

- оптимізаційні (призначені для вибору найкращого варіанта з певного числа варіантів виробництва, розподілу чи споживання).

Одними з найбільш поширених економіко-математичних моделей є оптимізаційні, які, як правило, використовуються на мікрорівні.

Відмінними ознаками оптимізаційних моделей є:

- наявність одного або декількох критеріїв оптимальності; найбільш типовими критеріями в економічних оптимізаційних задачах є: максимум доходу або прибутку, мінімум витрат, мінімальний час для виконання завдання та інші;

- система обмежень, яка формується, виходячи зі змістовної постановки задачі, і являє собою систему рівнянь або нерівностей.

Оптимізаційна задача в загальному вигляді:

Знайти значення змінних 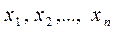, які задовольняють системі нерівностей (рівнянь):

g_i ( 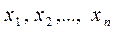) ≤ b_i, i = 1,2,…,m, (1)

і приводять до максимуму (або мінімуму) цільову функцію:

F = f ( 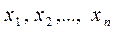) → max (min). (2)

Умови невід'ємності змінних, якщо вони є, входять в обмеження (1).

У задачі математичного програмування функцію F= f ( 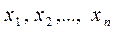) називають цільовою функцією; систему нерівностей (1) – обмеженнями завдання.

Для розв’язання завдання (1) – (2) застосовуються методи математичного програмування.

Якщо цільова функція (2) та обмеження (1) представлені лінійними функціями, то така задача є задачею лінійного програмування.

Якщо, виходячи зі змістовного сенсу, її рішення має бути виражене цілими числами, то це завдання цілочисельного лінійного програмування.

Якщо цільова функція (2) і (або) обмеження (1) задаються нелінійними функціями, то маємо задачу нелінійного програмування.

Якщо функції f і (або) gi у виразах (2) і (1) залежать від параметрів, то отримуємо задачу параметричного програмування, якщо ці функції носять випадковий характер, - задачу стохастичного програмування.

Якщо мова йде про процес поетапного прийняття рішень, що розгортається в часі, то маємо задачу динамічного програмування.

З перерахованих методів математичного програмування найбільш поширеним і розробленим є лінійне програмування.

Питання для самоконтролю:

1. У чому різниця між статичними і динамічними математичними моделями, що використовуються в економіці?

2. Що таке стохастичні моделі? Наведіть приклади.

3. Де застосовуються трендові моделі в економіці?

Рекомендована література:

основна: [1, 2, 4, 5, 6, 9];

додаткова: [3, 7, 8, 10-21].