Симплексний метод розв'язування задач лінійного програмування
Симплексний метод є універсальним методом розв’язання задач лінійного програмування. Свою назву метод бере від слова «симплекс» (найпростіші багатокутник, багатогранник). N-мірні симплекси розглядав американський вчений Дж. Данциг при розробці ним у 50-і рр. ХХ ст. даного методу рішення ЗЛП.
Сутність симплекс-методу полягає в тому, щоб, знайшовши будь-яким способом початкове дозволене базисне рішення (яку-небудь із вершин багатогранника ОДР), переходити до наступного, більш оптимального базисного рішення (наступної вершини ОДР), перевіряючи на кожному кроці виконання критерію оптимальності.
Застосовують симплекс-метод до задачі канонічного (стандартного) виду, в якій всі обмеження – рівності з невід’ємною правою частиною, і на всі змінні накладається умова невід'ємності.
Знаходження початкового допустимого базисного рішення і перехід до наступного опорного рішенням проводяться на основі методу Жордана-Гаусса для системи лінійних рівнянь канонічної форми ЗЛП.
Алгоритм симплекс-методу складається з кількох етапів, які розглянемо на прикладі.
Приклад. На підприємстві є дві категорії робітників: основні і допоміжні. Норми витрат праці (в деяких одиницях виміру трудомісткості) на виробництво одиниці двох видів продукції, наявність трудових ресурсів на підприємстві та ціни одиниць продукції наведені в таблиці 1.
Таблиця 1 – Вихідні дані
| Категорія персоналу | Норми витрат праці на виробництво одиниці продукції | Наявні трудові ресурси | |
| П1 | П2 | ||
| Основні | |||
| Допоміжні |
Ціна одиниці продукції становить відповідно 2 грн. і 3 грн. Необхідно скласти такий план виробництва продукції, при якому загальна виручка підприємства від її реалізації буде найбільшою.
У розглянутому прикладі цільова функція, що виражає вимогу максимізації прибутку, має вигляд:
F = 2х1 + 3х2 ® max.
Обмеження визначають залежність між величинами необхідних і наявних ресурсів і можуть бути записані так:
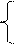 1х1 + 3х2 £ 300;
1х1 + 3х2 £ 300;
х1 + х2 £ 150.
Граничні умови показують, в яких межах можуть бути знайдені величини. Оскільки жодних вимог щодо кількості вироблених продуктів в прикладі не висувається, то граничні умови являють собою вимоги невід'ємності змінних, тобто:
х1 ³ 0, х2 ³ 0.
Отже, математична модель задачі в симетричному вигляді представляється наступним чином:
F = 2х1 + 3х2 ® max
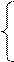 1х1 + 3х2 £ 300;
1х1 + 3х2 £ 300;
х1 + х2 £ 150.
х1 ³ 0, х2 ³ 0
Для приведення її до канонічної (стандартної) форми в ліву частину кожної з нерівностей введемо додаткову змінну. Отримаємо:
F = 2х1 + 3х2 + 0х3 + 0х4 → max
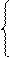 х1 + 3х2 + х3 = 300;
х1 + 3х2 + х3 = 300;
х1 + х2 + х4 = 150.
xj ≥ 0 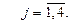
Очевидно, додаткові змінні х3, х4, які дорівнюють різниці між правою і лівою частинами обмежень, являють собою можливий резерв відповідного ресурсу.
Матрична форма запису моделі:
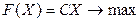 (6)
(6)
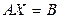 (7)
(7)
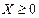 , (8)
, (8)
де
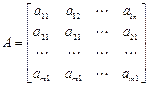 - Матриця умов завдання.
- Матриця умов завдання.
1. Визначення початкового (опорного) плану ЗЛП.
Перепишемо систему обмежень у вигляді:
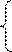 |
х3= 300 – (х1 + 3х2);
х4= 150 – (х1 + х2).
В отриманій системі змінні, що знаходяться у правій частині (х1, х2), називаються вільними (неосновними). А змінні, розташовані зліва (тобто додаткові змінні х3, х4), називаються базисними. Дорівнюючи вільні змінні нулю, отримаємо базисне рішення. вважаючи х1 = 0, х2 = 0, отримаємо значення базисних змінних х3 = 300, х4 =150.
Таким чином, отримано початковий опорний план: Х0 = (0; 0; 300; 150).
При цьому цільова функція F, очевидно, дорівнює нулю.
2. Побудова симплексної таблиці.
Отримане рішення внесемо до таблиці:
| Базис | сi (цільов. ф-ція) | План (bi) | α | |||||
| х1 | х2 | х3 | х4 | |||||
| х3 | ||||||||
| х4 | ||||||||
| ∆j= zj - cj | ||||||||
3. Перевірка опорного плану.
Умова оптимальності: опорне рішення ЗЛП на максимум (мінімум) цільової функції є оптимальним тоді і тільки тоді, коли всі Δj ненегативні (непозитивні): 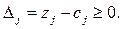 Обчислимо величину оцінок для розглянутого прикладу:
Обчислимо величину оцінок для розглянутого прикладу:
∆1 = z1 – c1 = (0 ∙ 1 + 0 ∙ 1) - 2 = -2;
∆2 = z2 – c2 = (0 ∙ 3 + 0 ∙ 1) - 3 = -3;
∆3 = z3 – c3 = (0 ∙ 1 + 0 ∙ 0) - 0 = 0;
∆4 = z4 – c4 = (0 ∙ 0 + 0 ∙ 1) - 0 = 0.
| Базис | сi (цільоев. ф-ція) | План (bi) | α | |||||
| х1 | х2 | х3 | х4 | |||||
| х3 | ||||||||
| х4 | ||||||||
| ∆j= zj - cj | -2 | -3 | ||||||
Елементи цільового рядка не відповідають умові оптимальності, оскільки серед них є негативні величини. Це свідчить про можливість збільшення цільової функції, отже, опорне рішення не є оптимальним.
4. Перехід до нового опорного плану.
Перехід до нового опорного плану здійснюється шляхом заміни базисних змінних. При цьому обрана для введення в число базисних вільна змінна називається введеною, а видалена в розряд вільних базисна змінна – виведеною.
1. Вибір тієї, що вводиться до числа базисних змінних визначається умовою оптимальності: вводима до числа базисних змінна визначається максимальною за абсолютною величиною негативною оцінкою при розв’язанні задачі на максимум цільової функції і найбільшою позитивною оцінкою – при розв’язанні задачі на мінімум. Відповідний стовпчик коефіцієнтів у симплекс-таблице називається ключовим.
У цільовому рядку є негативні оцінки, максимально по модулю з яких - Δ2 = -3, тому, слідуючи правилу в якості введеної змінної треба взяти х2.
2. Вибір тієї, що виводиться з числа базисних (в розряд вільних) змінної здійснюється наступним чином. Змінна, що виводиться з числа базисних, незалежно від спрямованості оптимізації, визначається за мінімальним симплекс-відношенням. Симплекс-відношення являє собою відношення елементів підсумкового стовпця «Опорний план» симплекс-таблиці до відповідних позитивних елементів ключового стовпця. Якщо елемент ключового стовпця ≤ 0, то симплекс-відношення не розраховується (ставиться прочерк або знак ∞). Якщо в ключовому стовпці всі елементи ≤ 0, це свідчить про те, що ЗЛП не має рішення виходячи з необмеженості цільової функції.
Відповідний виведеній змінній рядок в симплекс-таблице називається ключовим.
Так, у нульовій симплексній таблиці розв'язуваної задачі симплекс-відношення для базисної змінної х3 дорівнює 300: 3 = 100, а для базисної змінної х4 – 150: 1 = 150. Ці значення записуються в останній графі симплексної таблиці. Мінімальне з симплекс-відношень визначає ключовий рядок і виведену з числа базисних змінну – це х3.
Елемент, що знаходиться на перетині ключовий рядка і ключового стовпця (число 3), називається ключовим елементом і буде використаним для перерахунку елементів симплекс-таблиці.
| Базис | сi (цільов.ф-ція) | План (bi) | α | |||||
| х1 | х2 | х3 | х4 | |||||
| ←х3 | ||||||||
| х4 | ||||||||
| ∆j= zj - cj | -2 | -3 | ||||||
Наступний крок на етапі переходу до нового опорного плану – перерахунок всіх елементів таблиці, який виконується за правилом, що складається з двох частин.
1) елементи ключового рядка діляться на ключовий елемент. Отримані таким чином величини поміщають в нову таблицю. Так в першій симплексній таблиці елементи рядка х2 дорівнюють:
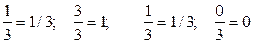 .
.
2) всі інші елементи, включаючи цільовий рядок, перераховуються за правилом «прямокутного трикутника»:
| Базис | сi (цільов.ф-ція) | План (bi) | α | |||||
| х1 | х2 | х3 | х4 | |||||
| ←х3 | ||||||||
| х4 | ||||||||
| ∆j= zj - cj | -2 | -3 | ||||||
| →х2 | 1/3 | 1/3 | ||||||
| х4 | ||||||||
| ∆j= zj - cj | ||||||||
а) до стовпчика β записуються відношення елементів ключового стовпця до ключового елементу: 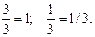
б) перерахунок елементів виконується відповідно до схеми:
анове = астаре – b∙с

|
|
|
де b – елемент, що знаходиться на перехресті стовпчика, що містить число, що перераховується, та ключового рядка;
с – елемент, що знаходиться на перехресті рядка, що містить число, що перераховується, та стовпчика β.
150-300·1/3=50; 1-1·1/3=2/3; 1-3·1/3=0; 0-1·1/3=-1/3; 1-0·1/3=1.
| Базис | сi (цільов.ф-ція) | План (bi) | α | β | ||||
| х1 | х2 | х3 | х4 | |||||
| ←х3 |  300 300
| |||||||
| х4 | 1/3 | |||||||
| ∆j= zj - cj | -2 | -3 | ||||||
| →х2 | 1/3 | 1/3 | ||||||
| х4 | ||||||||
| ∆j= zj - cj |
Отримані значення заносяться до нової симплекс таблиці:
| Базис | сi (цільов.ф-ція) | План (bi) | α | β | ||||
| х1 | х2 | х3 | х4 | |||||
| х3 | ||||||||
| х4 | 1/3 | |||||||
| ∆j= zj - cj | -2 | -3 | ||||||
| х2 | 1/3 | 1/3 | ||||||
| х4 | 2/3 | -1/3 | ||||||
| ∆j= zj - cj |
Розрахуємо величини оцінок:
∆1 = z1 – c1 = (3 ∙ 1/3 + 0 ∙ 2/3) - 2 = -1;
∆2 = z2 – c2 = (3 ∙ 1 + 0 ∙ 0) - 3 = 0;
∆3 = z3 – c3 = (3 ∙ 1/3 + 0 ∙ -1/3) - 0 = 1;
∆4 = z4 – c4 = (3 ∙ 0 + 0 ∙ 1) - 0 = 0.
Результати заносимо до таблиці:
| Базис | сi (цільов.ф-ція) | План (bi) | α | β | ||||
| х1 | х2 | х3 | х4 | |||||
| х3 | ||||||||
| х4 | 1/3 | |||||||
| ∆j= zj - cj | -2 | -3 | ||||||
| х2 | 1/3 | 1/3 | ||||||
| ←х4 | 2/3 | -1/3 | ||||||
| ∆j= zj - cj | -1 |
Оскільки серед оцінок ще є негативна Δ1 = -1, то робимо висновок про те, що нове рішення не є оптимальним. Змінна х1 тепер буде вводитися, х4 – виводитися (мінімальне симплекс-відношення дорівнює 75).
Виконавши перерахунок, приходимо до наступної симплексної таблиці.
100-50·1/2=75; 1/3-2/3·1/2=0; 1-0·1/2=1; 1/3-(-1/3·1/2)=1/2; 0-1·1/2=-1/2.
Розрахуємо оцінки:
∆1 = z1 – c1 = (3 ∙ 0 + 2 ∙ 1) - 2 = 0;
∆2 = z2 – c2 = (3 ∙ 1 + 2 ∙ 0) - 3 = 0;
∆3 = z3 – c3 = (3 ∙ 1/2 + 2 ∙ (-1/2)) - 0 = 1/2;
∆4 = z4 – c4 = (3 ∙ (-1/2) + 2 ∙ 3/2) - 0 = 3/2.
| Базис | сi (цільов.ф-ція) | План (bi) | α | β | ||||
| х1 | х2 | х3 | х4 | |||||
| ←х3 | ||||||||
| х4 | 1/3 | |||||||
| ∆j= zj - cj | -2 | -3 | ||||||
| →х2 | 1/3 | 1/3 | 1/2 | |||||
| ←х4 | 2/3 | -1/3 | ||||||
| ∆j= zj - cj | -1 | |||||||
| х2 | 1/2 | -1/2 | ||||||
| →х1 | -1/2 | 3/2 | ||||||
| ∆j= zj - cj | 1/2 | 3/2 |
У рядку оцінок симплексної таблиці виконується умова невід'ємності, що свідчить про досягнення оптимального рішення. Якщо в отриманому оптимальному плані оцінки всіх вільних змінних строго більше нуля, то оптимальний план є єдиним. Наявність нульових оцінок деяких вільних змінних в оптимальному плані свідчить про те, що він неєдиний.
Питання для самоконтролю:
1. Яким чином формується система обмежень задачі?
2. Що таке рівняння зв’язку?
3. Рішення економіко-математичної моделі – що це таке?
4. У чому різниця між допустимим рішенням та допустимим планом?
5. Які практичні задачі дозволяє розв’язати симплексний метод?
Рекомендована література:
основна: [1, 2, 4, 5, 6, 9];
додаткова: [3, 7, 8, 10-21].
Дата добавления: 2015-11-10; просмотров: 1564;
