Показатели вариации (колеблемости) признака
Для характеристики размера вариации признака используются абсолютные и относительные показатели. К абсолютным показателям вариации относятся:
• размах колебаний;
• среднее линейное отклонение;
• среднее квадратическое отклонение;
• дисперсия;
• квартильное отклонение.
Размах колебаний (размах вариации)
 ,
,
где хmах, xmln - соответственно максимальное и минимальное значения признака.
Величина показателя зависит от величины только двух крайних вариант и не учитывает степени колеблемости основной массы членов ряда.
Среднее линейное отклонение ( 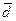 ) и среднее квадратическое отклонение (s) показывают, на сколько в среднем отличаются индивидуальные значения признака от среднего его значения.
) и среднее квадратическое отклонение (s) показывают, на сколько в среднем отличаются индивидуальные значения признака от среднего его значения.
Среднее линейное отклонение определяется по формулам:
а) для несгруппированных данных (первичного ряда)
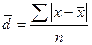 ;
;
б) для вариационного ряда
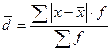 .
.
Среднее квадратическое отклонение (s) и дисперсия (s2) определяются так:
а) для несгруппированных данных
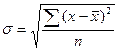 ;
; 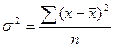 .
.
б) для вариационного ряда
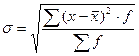 ;
; 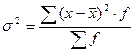 .
.
Формула для расчета дисперсии может быть преобразована:
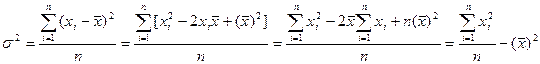 ,
,
т. е. дисперсия равна средней из квадратов индивидуальных значений признака минус квадрат средней величины. Следовательно,
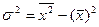 .
.
Среднее квадратическое отклонение по всей величине всегда превышает значение среднего линейного отклонения в соответствии со свойством мажорантности средних.
Квартильное отклонение ( 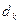 ) применяется вместо размаха вариации, чтобы избежать недостатков, связанных с использованием крайних значений:
) применяется вместо размаха вариации, чтобы избежать недостатков, связанных с использованием крайних значений:
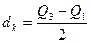 ,
,
где (Q3 и Ql - соответственно третья и первая квартили распределения.
Квартиль – значения признака, которые делят ранжированный ряд на четыре равные по численности части. Таких величин будет три: первая квартиль (Q1), вторая квартиль (Q2), третья квартиль (Q3). Вторая квартиль является медианой. Вычисление квартилей аналогично вычислению медианы.
Сначала определяют положение или место квартили:
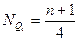 ;
; 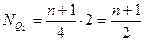 ;
; 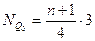 .
.
Затем по накопленным частотам в дискретном ряду определяют численное значение.
В интервальном ряду распределения сначала указывают интервал, в котором лежит квартиль, затем определяют ее численное значение по формуле
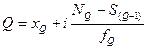 ,
,
где хQ - нижняя граница интервала, в котором находится квартиль;
S(Q-1) - накопленная частота интервала, предшествующего тому, в котором находится квартиль;
fQ - частота интервала, в котором находится квартиль.
При сравнении колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях с различной величиной средней арифметической используются относительные показатели вариации. Они вычисляются как отношение абсолютных показателей вариации к средней арифметической (или медиане) и чаще всего выражаются в процентах.
Формулы расчета относительных показателей вариации следующие:
коэффициент осцилляции 
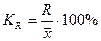 ;
;
относительное линейное отклонение 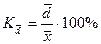 ;
;
коэффициент вариации 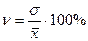 ;
;
относительный показатель квартильной вариации 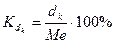 , или
, или 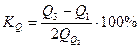 .
.
Наиболее часто применяется коэффициент вариации. Его применяют не только для сравнительной оценки вариации, но для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному).
Сложение дисперсий изучаемого признака
Изучая дисперсию интересующего нас признака в пределах исследуемой совокупности и опираясь на общую среднюю в расчетах, нельзя оценить влияние отдельных факторов, определяющих колеблемость индивидуальных значений (вариант) признака. Это можно сделать при помощи метода группировок, когда единицы изучаемой совокупности подразделяются на однородные группы по признаку-фактору. При этом кроме общей средней для всей совокупности исчисляются средние по отдельным группам ( групповые или частные средние) и три показателя дисперсии:
Ø общая дисперсия;
Ø межгрупповая дисперсия;
Ø средняя внутригрупповая дисперсия.
Величина общей дисперсии ( 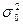 ) характеризует вариацию признака под влиянием всех факторов, формирующих уровень признака у единиц данной совокупности и определяется по формуле
) характеризует вариацию признака под влиянием всех факторов, формирующих уровень признака у единиц данной совокупности и определяется по формуле
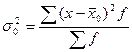 ,
,
где 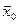 - это общая средняя арифметическая для всей изучаемой совокупности.
- это общая средняя арифметическая для всей изучаемой совокупности.
Межгрупповая дисперсия(дисперсия групповых средних 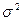 ) отражает систематическую вариацию, т. е. те различия в величине изучаемого признака, которые возникают под влиянием фактора положенного в основу группировки. Межгрупповая дисперсия определяется по формуле
) отражает систематическую вариацию, т. е. те различия в величине изучаемого признака, которые возникают под влиянием фактора положенного в основу группировки. Межгрупповая дисперсия определяется по формуле
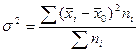 ,
,
где хi - средняя по отдельной группе;
ni - число единиц в определенной группе.
Средняя внутригрупповая дисперсия( 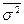 ) характеризует случайную вариацию, возникающую под влиянием других, неучтенных факторов, и не зависит от условия (признака-фактора), положенного в основу группировки.
) характеризует случайную вариацию, возникающую под влиянием других, неучтенных факторов, и не зависит от условия (признака-фактора), положенного в основу группировки.
Дата добавления: 2015-11-10; просмотров: 2033;
