Расчет показателей вариации
| Тарифный разряд, х | Число рабочих, f | 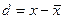
| 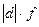
| 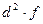
|
| -1,8 -0,8 +0,2 +1,2 +2,2 | 7,2 4,0 1,8 4,8 4,4 | 12,96 3,20 0,36 5,76 9,68 | ||
| Итого | 22,2 | 31,96 |
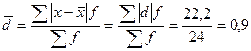 разряда;
разряда;
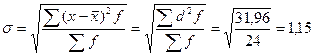 разряда;
разряда;
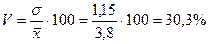
Следовательно, индивидуальные значения отличаются в среднем от средней арифметической на 1,15 разряда, или на 30,3%.
Среднее квадратическое отклонение превышает среднее линейное отклонение в соответствии со свойствами мажорантности средних.
Значение коэффициента вариации (30,3%) свидетельствует о том, что совокупность достаточно однородна.
Как видно на рис. 3.1, распределение рабочих по тарифному разряду несимметрично, поэтому определяется показатель асимметрии:
 .
.
Следовательно, асимметрия левосторонняя, незначительная.
2. Распределение грузовых автомобилей автотранспортного предприятия по величине суточного пробега за 10 мая следующее (табл 5).
Таблица 5
| Суточный пробег (км), х | 100-125 | 125-150 | 150-200 | Итого |
| Число автомобилей, f |
Требуется построить вариационный ряд с равными интервалами в 20 км.
Решение
Построение нового ряда с равными интервалами осуществляется в следующей последовательности.
1. Записывается макет таблицы нового ряда (табл. 6).
Таблица 6
| Суточный пробег (км), х | 100-120 | 120-140 | 140-160 | 160-180 | 180-200 | Итого |
| Число автомобилей, f |
2. Определяется абсолютная плотность имеющегося распределения с неравными интервалами:
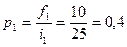 ;
; 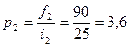 ;
; 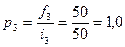 .
.
3. Находятся частоты для каждой группы нового ряда по формуле:
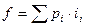 ;
;
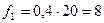 ;
;
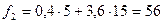 ;
;
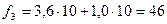 ;
;
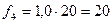 ;
;
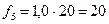 .
.
4. Оформляется новый ряд распределения с равными интервалами.
Распределение грузовых автомобилей автотранспортного предприятия по величине суточного пробега за 10 мая представлено в табл. 7.
| Суточный пробег (км), х | 100-120 | 120-140 | 140-160 | 160-180 | 180-200 | Итого |
| Число автомобилей, f |
3. Дневная производительность труда рабочих бригады, выполняющих одинаковую операцию по обработке детали № 408, следующая (табл. 8).
Таблица 8
| Дневная производительность труда (шт.), х | Итого | ||||||
| Число рабочих, f |
Определить численное значение медианы.
Решение
Совокупность содержит четное число значений признака, по
этому медиана определяется по формуле:
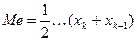 ; k = n:2 = 10.
; k = n:2 = 10.
Следовательно
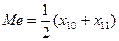 .
.
Для определения численных значений х10 и х11 исчисляются накопленные частоты (табл. 9).
Таблица 9
| Дневная производительность труда (шт.), х | ||||||
| Число рабочих, f |
х10 = 20 шт.; х11 = 21.
Отсюда,
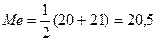 шт.
шт.
4.Дисперсия признака равна 600. Объем совокупности равен 10. Сумма квадратов индивидуальных значений признака равна 6250.
Найти среднюю величину.
Решение
Для нахождения средней величины воспользуемся формулой
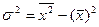 ,
,
где 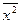 - средняя арифметическая из квадратов индивидуальных значений признака;
- средняя арифметическая из квадратов индивидуальных значений признака;
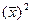 - квадрат среднего значения признака.
- квадрат среднего значения признака.
Тогда
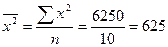 .
.
Средняя величина признака
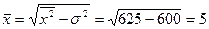 .
.
Дата добавления: 2015-11-10; просмотров: 6929;
