Тема 1.6 Нагрев неограниченного цилиндра
Решение задачи нагрева цилиндра произведем с помощью преобразования Ханкеля
 (81)
(81)
Краевые условия
T(r,0)=f(r); (82)
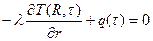 (83)
(83)
 (84)
(84)
Для решения задачи воспользуемся конечным интегральным преобразованием Ханкеля
 (85)
(85)
Где p – корень характеристического уравнения
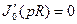 (86)
(86)
Переход от изображения к оригиналу осуществляется по формуле
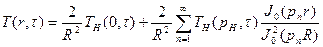 (87)
(87)
Применяя преобразование (85) к дифференциальному уравнению (81) с учётом ГУ (83), (84) получим
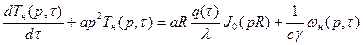 (88)
(88)
Где 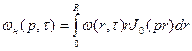 (89)
(89)
Решение обыкновенного диф. уравнения имеет вид
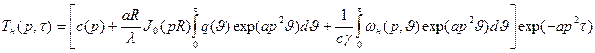 (90)
(90)
Для определения постоянной C(p) воспользуемся начальным условием (81). Из решения (89) следует, что при 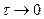
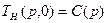 (91)
(91)
Кроме того, по определению изображения имеем
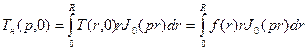 (92)
(92)
Следовательно
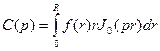 (93)
(93)
Если вместо C(p) подставим выражение (93) в решение (90), то получим решение задачи для изображения 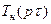
Для перехода к оригиналу 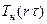 из решения (89)
из решения (89)
 (95)
(95)
Где 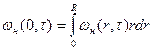 (96)
(96)
Подставив значение 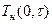 и
и 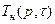 в формулу (97) получим решение
в формулу (97) получим решение
 (97)
(97)
Обозначим 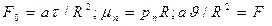
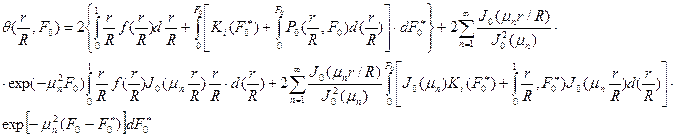 (98)
(98)
Где 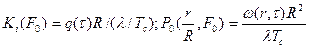 (99)
(99)
 - корни характеристического уравнения
- корни характеристического уравнения 
Если начальное распространение темперfтуры равномерное 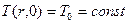 , а
, а 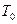 принята равной 0, то при
принята равной 0, то при  решение (98) можно записать так
решение (98) можно записать так
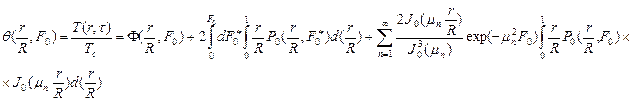 (100)
(100)
Где  (101)
(101)
Частные случаи
1. Постоянный источник тепла 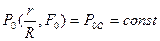
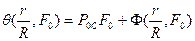 (102)
(102)
2. Источник тепла – параболическая функция
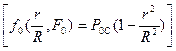 (103)
(103)
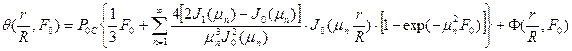 (104)
(104)
Где 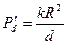 - критерий Предводителева
- критерий Предводителева 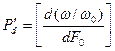
Дата добавления: 2015-08-21; просмотров: 883;
