Тема 1.5 Нагрев неограниченной пластины. Решение методом преобразования Фурье

Дана неограниченная пластина толщиной 2R при температуре 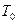. Теплообмен с окружающей средой происходит при ГУ2. Нагрев осуществляется переменным источником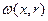

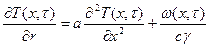(60)

НУ T(x,0)=f(x) (61)

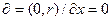(62)

ГУ2 принимаем в виде

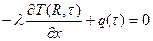(63)

Решение найдём методом интегрального преобразования Фурье

Воспользуемся косинус - преобразованием Фурье

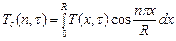(64)

И формулой перехода от изображения функции 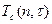к её оригиналу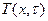

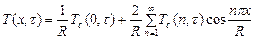(65)

Умножая обе части дифференциального уравнения (60) на 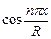и интегрируя в пределах от 0 до R с учётом ГУ(72) и(73) получим

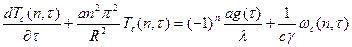(66)

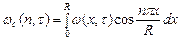Где (67)

Решение этого уравнения б

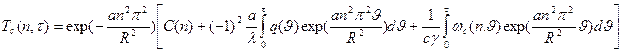
(68)

Для определения C(n) воспользуемся Н.У. (71)

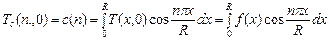(69)

Тогда

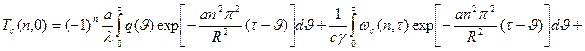
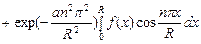(70)

Для удобства перехода к оригиналу по соотношению (65) применяем решение для изображение (68) в виде

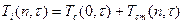(71)

Причём во втором слагаемом n=1,2,3….

Имеем:

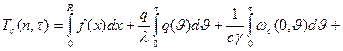
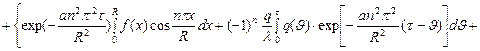
(72)

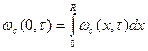Где (73)

Переход от изображения 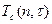к оригиналу производим по формуле (65)

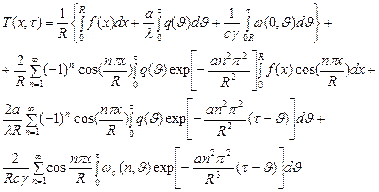
(74)

Решение (74) является общим решением поставленной задачи

Решение в обобщённых переменных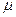

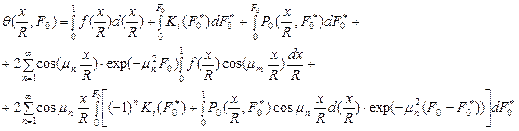
(75)

Здесь ; ;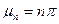

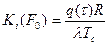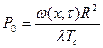
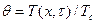
Из (75) можно получить ряд интересных для практически частных решений

1.

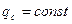
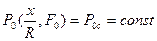
(76)

Где 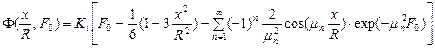(77) является решением задачи при отсутствии источников тепла

2. источник тепла – линейная функция от координаты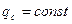

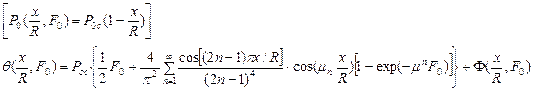
(78)

3. Источник тепла – линейная функция времени

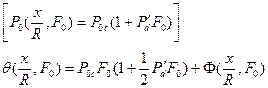
(79)

Где 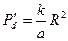- критерий Предводителева, равный максимальной скорости изменения относительной удельной мощности источника тепла по числу Фурье

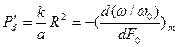(80)

k- постоянная, численно равная максимальной относительной скорости изменения удельной мощности источника тепла, - удельная мощность источника тепла при