Операционные методы.

Для многих задач теплопроводности использование классических методов оказывается неэффективным, например применение метода разделения переменных для задач с внутренними источниками тепла.

Основные правила и теоремы операционного исчисления были получены М.Вищенко-Захарченко и Хевисвйдом. Наибольшее распространение они получили в электротехнике благодаря работам Хевисайда.

Операционный метод Хевисвйда равнозначен методу интегрального преобразования Лапласа.

Метод преобразования Лапласа состоит в том, что изучается не сама функция (оригинал), а её видоизменение (изображение).

Интегральное преобразование 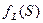функции 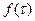определяется формулой

(40)

Здесь S может быть комплексным числом; но при этом вещ-я часть больше 0.

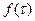- оригинал; 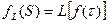- изображение функции . Чтобы изображение существовало необходимо, интеграл (51) должен сходиться.

Если задача решена в изображениях, то оригинал определяется по изображению (обр-е преобр-е) с помощью формулы обращения

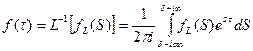(41)

Вместо формулы (52) для определения оригинала функции по её изображению можно воспользоваться следующей формулой обращения

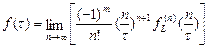(41.а)

Эта формула даёт возможность получить оригинал функции лишь при помощи операция дифференцирования и перехода к пределу.

1. Если изображение представляет собой функцию

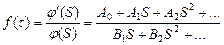(42)

которая является частичным случаем двух целых трансцендентных функций, то по теореме разложения имеем

(43)

где 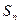- простые корни функции 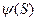; при этом знаменатель не содержит свободных членов и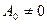

2. Если изображение 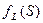представляет собой отношение двух номиналов (дробно-рациональная функция), причём степень номинала 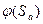меньше степени номинала 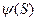, и номинал 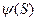имеет корни кратности K в точках 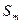, то

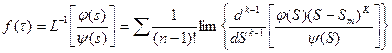
где сумма берётся по всем корням 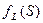. Если все корни простые, т.е. все К равны единице, то формула (5 ) переходит в (43)

Интегральное преобразование Лапласа имеет свои недостатки. В частности, трудности возникают при решении задач, где условия заданы в виде функции пространственных координат, или решении многомерных задач.

В этой связи был предложен ряд методов интегральных преобразований по пространственным координатам в соответствии с геометрической формой тела.

Если преобразование берётся по пространственной координате х, то интегральное преобразование функции 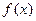может быть представлено так:

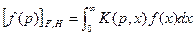(44)

Если ядро преобразования K(p,x) берётся в виде 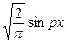или 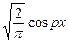, то это интегральное преобразование называется соответственно синус- или косинус- преобразованием Фурье.

Если же ядром преобразования выбрана функция Бесселя 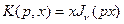, то оно называется преобразованием Ханкеля.

Комплексное преобразование Фурье удобно применять для тел неограниченной протяжённости, синус- преобразование Фурье следует использовать , когда на поверхности тела задано значение формулами, т.е. при ГУ!, а косинус – преобразование Фурье, когда решается диф. уравнения переноса при ГУ2. Преобразования Ханкеля применимы в том случае, когда тело имеет осевую симметрично. Практическое применение названных интегральных преобразований при наличии подробных таблиц изображения не вызывают особых затруднений.

Переход от изображений к оригиналам можно осуществить по формулам обращения для:

Комплексное преобразование Фурье

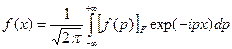(45)

Синус-преобразование Фурье

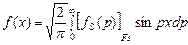(46)

Косинус-преобразование Фурье

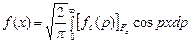(47)

Преобразование Ханкеля

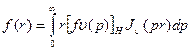(48)

Рассмотренные интегральные преобразования применимы для тел полуограниченной протяженности.

Конечные интегральные преобразования

Ограниченность интегральных преобразований Фурье, Ханкеля, и отчасти Лапласа, с одной стороны, и острая необходимость в решении задач с конечной областью изменения переменных, с другой, привели к созданию методов конечных интегральных преобразований. Они более предпочтительны даже для задач, решаемых классическими методами.

Идея метода конечных интегральных преобразований предложена Н.С. Коммековым

(49)

Дальнейшая проработка вопросов метода конечных интегральных преобразований нашла отражение в трудах Гриабарга Г.А., Следдона, Трантера, Дёга (Дейг) и др.

Если граница интегрирования заключается между 0 и е, ядро конечных синус - и косинус - преобразований Фурье, а также преобразования Ханкеля соответственно имеют вид:

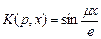(50)

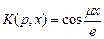(51)

При ГУ1 и ГУ2 , а при ГУ3 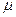является корнями уравнения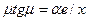

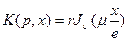(52)

где 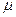- корень уравнения (ГУ1), а при ГУ3 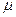определяется из уравнения

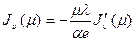(53)

Формула обращения обычно находится при помощи разложения функции в ряды по ортогональным функциям соответствующей задачи Штурма-Лиувилля. Поэтому решения, полученные этими методами имеют те же принципиальные недостатки, как и решения, полученные классическими методами. Так, формулы обращения имеют вид:

Для синус-преобразования Фурье

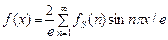(54)

Для косинус-преобразования Фурье

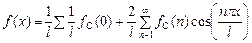(55)

При ГУ2 и при ГУ3, суммирование ведётся по всем положенным корням уравнения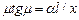

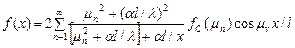(56)

Для преобразования Ханкеля при корнях из уравнения

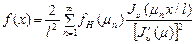(57)

Или, если корни определяются по (53)

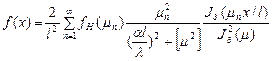(58)

Преобразование Ханкеля (52) применяется для решения задач теплопроводности для цилиндра. Для малого цилиндра в преобразованиях Ханкеля ядро преобразования K(p,x) берётся в ином виде

Методы интегрального преобразования дают возможность получить ряд закономерностей протекания физических процессов на основе анализа решения для усреднённых значений исследуемой физической величины (анализ решения для изображения). Это обстоятельство сближает данные аналитические методы с методами теории подобия.