Тема 1.1Математическое моделирование системы индукционного нагрева.

Система индукционного нагрева представляет собой, в общем случае, источник питания, индуктор, нагреваемое тело и окружающую среду.

Источник питания будь то генератор повышенной частоты, тиристорный преобразователь частоты, ламповый генератор или просто понижающий трансформатор, в ряде является довольно сложным. Рассматривать его мы не будем, т.к. отдельные стороны его функционирования излагались в курсе « Источники питания ЭТУС», и кроме того, существует теория электропривода, вполне позволяющая выяснить характер поведения источника питания как объекта управления.

Таким образом, будем рассматривать систему индуктор - нагреваемое тело – окружающая среда. Эта система описывается системами уравнений для электромагнитного и теплового полей.

Прежде чем записать уравнение из этих систем сделаем ряд общепринятых для таких задач допущений (без них задача становится гораздо сложнее при незначительном выигрыше в точности).

1. Электромагнитное поле принимается квазистационарным. Под этим понимается отсутствие запаздывания электромагнитной волны в воздухе (но не в металле). В иной формулировке длины ЭМ – волны в воздухе много больше геометрического размера системы (например длины индуктора). Это допущение позволяет пренебречь токами смещения по сравнению с токами в проводниках.

2. Расчет установившихся ЭМ - процессов можно проводить для величин, меняющихся по гармоническому закону. При этом ошибка в определении интегральных и распределенных энергетических параметров невелика. Это позволяет широко использовать символический метод для расчета ЭМ – полей в нелинейных ферромагнитных средах.

3. Потери на гистерезис при нагреве ферромагнитных тел много меньше, чем на вихревые токи. Поэтому можно считать зависимость μ(Н) однозначной, а саму проницаемость – действительной величиной.

4. Потери на гистерезис и вихревые токи в магнитопроводе не оказывают заметного влияния на ЭМ – поле вне его и их возможно учитывать отдельно при расчете теплового режима в магнитопроводе.

Теперь запишем систему уравнений, описывающую электромагнитный процесс в поглощающих средах

rot H=J=γE; (1)

rot E= - 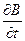= - 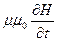; (2)

div B=0; (3)

div D=div( 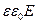)= . (4)

Здесь Н, В, Е и D – векторы напряженности и индукции магнитного и электрического полей; J – вектор плотности тока.

Уравнение (1) представляет собой обобщенный закон полного тока в дифференциальной форме. Уравнение (2) есть закон электромагнитной индукции в дифференциальной форме. Оба эти уравнения выражают тот факт, что переменные электрические и магнитные поля существуют совместно и являются разными сторонами единого электромагнитного процесса. Уравнение (3) является выражением принципа непрерывности магнитного потока, означающего отсутствие источников магнитного поля, а уравнение (4) представляет собой дифференциальную форму теоремы Гауса, утверждающей, что источником электрического поля являются электрические заряды.

Температурное поле описывается дифференциальным уравнением в частных производных, вид которого зависит от формы нагреваемого тела. Для тела прямоугольной формы уравнение примет вид

. (5)

Условия теплообмена, начальные условия записываются в виде уравнений, соответствующих граничным условиям 1, 2 и 3-го рода. Например, если принять участвующей в теплообмене только одну грань с координатами х=Х; у,z=var, то уравнения будут иметь вид

ГУ1: T(x,y,z)= 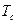; (6)

ГУ2: 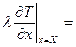q; (7)

ГУ3: 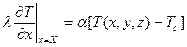. (8)

Более сложный вид ГУ, например, теплообмен излучением целесообразно привести к виду (7) или (8). Это упростит аналитическое решение.

ГУ4: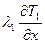

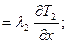
Совместное решение уравнений (1)-(4) и (5)-(8) является очень сложной задачей. Но, к счастью, этого и не требуется для задач в области ЭТУ. Чаще всего решение электромагнитной и тепловой задач производится отдельно, что вполне допустимо ввиду большой инерционности тепловых процессов по сравнению с электромагнитными. Кроме того, зависимости свойств материала от температуры в большинстве своем ( кроме μ=f(τ) ) является близкими к линейным, что позволяет вводить в процессе решения усредненные параметры.

На основании вышесказанного решение электромагнитной и тепловой задач будем рассматривать раздельно.

Кроме рассмотренных двух задач в процессе нагрева возникает еще и задача термонапряжений, которые в отдельных случаях могут привести к разрушению нагреваемого тела. Эту задачу мы рассмотрим в численных методах.