Тема 1.2 Тепловая задача. Основные положения. Критерии и числа подобия
В настоящее время существует немало как аналитических , так и численных методов решения тепловых задач для тел цилиндрической и прямоугольной формы. В случае нагрева тел более сложной формы для решения пригодны только численные методы. Тем не менее, использование аналитических методов для тел правильной цилиндрической или прямоугольной формы (параллелепипед) вполне оправдало исходя и из затрат на создание модели, так и из удобства при решении задач управления.
Основные положения.
Градиент температуры есть вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры, т. е.
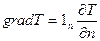 , (9)
, (9)
где 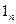 - единичный вектор, направленный по нормали в сторону возрастания температуры.
- единичный вектор, направленный по нормали в сторону возрастания температуры.
Градиент обозначается также символом (набла). Составляющие градиента по осям декартовых координат равны соответствующим частным производным так что
 . (10)
. (10)
Выражение в квадратных скобках в формуле (5) можно записать как 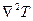 .
.
Основной закон теплопроводности Фурье.
Передача тепла теплопроводностью по нормали к изотермической поверхности от мест с большей температурой к местам с меньшей температурой.
Количество тепла, проходящее в единицу времени и отнесенное к единице площади изотермической поверхности, называется плотностью теплового потока
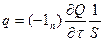 , (11)
, (11)
где 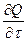 – количество тепла, проходящее в единицу времени или скорость теплового потока; S – площадь поверхности.
– количество тепла, проходящее в единицу времени или скорость теплового потока; S – площадь поверхности.
Закон: Плотность теплового потока прямо пропорциональна градиенту температуры
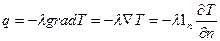 , (12)
, (12)
где λ – коэффициент теплопроводности.
Коэффициент теплопроводности равен количеству тепла, протекающего в единицу времени через единицу поверхности при перепаде температуры на единицу длины нормали, равном одному градусу.
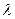 [Вт/(мград)]
[Вт/(мград)]
Коэффициент теплопроводности зависит от температуры для металлов он линейно убывает; для газов увеличивается; для жидкостей, кроме воды и глицерина, убывает.
Материалы с 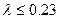 [Вт/(мград)] называются теплоизоляционными.
[Вт/(мград)] называются теплоизоляционными.
Кроме λ используется коэффициент температуропроводности a
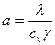
Коэффициент а температуропроводности равен количеству тепла, протекающего в единицу времени через единицу поверхности, при перепаде объемной концентрации внутренней энергии в 1 Дж/м³ на единицу длины нормали.
Критерии и числа подобия.
Теория подобия дает общий метод непосредственного преобразования выражений, содержащих дифференциальные операторы, к простейшим алгебраическим выражениям. Суть этого метода заключается в том, реальный процесс заменяется простейшей условной схемой, в которой все дифференциальные операторы сохраняют постоянные значения в пространстве и во времени.
Критерий Био
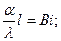
l - толщина пластины; 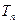 - температура поверхности;
- температура поверхности; 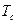 - температура среды.
- температура среды.
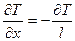 ;
; 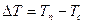 ;
; 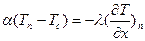 ; (13)
; (13)
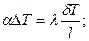
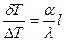 . (14)
. (14)
Соотношение между температурным переходом 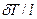 и температурным напором
и температурным напором  определяется непосредственно выражением
определяется непосредственно выражением 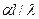 .
.
Понятие теплотехнически тонких тел.
В случае, когда термическое сопротивление отдачи тепла телом 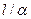 много больше удельного термического сопротивления переносу тепла теплопроводностью внутри тела от его поверхности к середине
много больше удельного термического сопротивления переносу тепла теплопроводностью внутри тела от его поверхности к середине 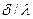 , то есть когда
, то есть когда
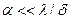 , (15)
, (15)
где 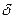 - половина толщины тела, тело называется теплотехнически тонким.
- половина толщины тела, тело называется теплотехнически тонким.
Во сколько раз 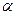 должна быть меньше, чем
должна быть меньше, чем 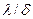 конкретной общепринятой цифры нет, да она зависит от требований к заданному перепаду. В каждом случае расчетчик решает сам, является ли тело теплотехнически тонким. Приближенно можно принять
конкретной общепринятой цифры нет, да она зависит от требований к заданному перепаду. В каждом случае расчетчик решает сам, является ли тело теплотехнически тонким. Приближенно можно принять 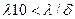 . Такому соотношению соответствует значение критерия Био Bi<0.25.
. Такому соотношению соответствует значение критерия Био Bi<0.25.
Критерий Фурье
Для одномерной задачи имеем
 . (16)
. (16)
Заменим 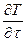 на
на  , а
, а 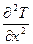 на
на 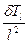 (индексы
(индексы 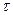 и l означают соответственно изменение температуры за время
и l означают соответственно изменение температуры за время 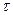 и на протяжении l).
и на протяжении l).
Тогда запишем
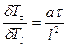 ; (17)
; (17)
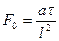 , (18)
, (18)
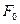 - обобщенное время. Его можно назвать критерием гомохронности (однородность по времени; если для двух систем отношение
- обобщенное время. Его можно назвать критерием гомохронности (однородность по времени; если для двух систем отношение 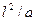 имеет одно и то же значение, то для них гомохронность переходит в синхронность).
имеет одно и то же значение, то для них гомохронность переходит в синхронность).
Правильнее назвать 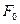 не критерием, а обобщенной переменной или числом Фурье.
не критерием, а обобщенной переменной или числом Фурье.
Критерий Померанцева
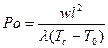 . (19)
. (19)
Критерий Кирпичева
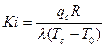 . (20)
. (20)
Число Нуссельта
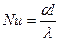 . (21)
. (21)
Число Нуссельта похоже на Bi, но здесь 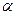 является неизвестной величиной; используется в задачах для жидкости.
является неизвестной величиной; используется в задачах для жидкости.
Обобщенная (относительная) температура
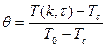 (22)
(22)
(безразмерная).
Дата добавления: 2015-08-21; просмотров: 1223;
