Тема 1.7 Нагрев цилиндра конечных размеров
 . (105)
. (105)
Если имеется симметрия относительно оси z, то оператор 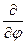 тождественно равен нулю, тогда получим
тождественно равен нулю, тогда получим
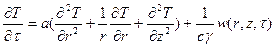 . (106)
. (106)
1). Рассмотрим решение уравнения для конечного цилиндра длиной l при ГУ2 на боковой поверхности.
Положим, что один из торцов (z=0) теплоизолирован.
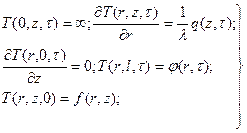 (107)
(107)
Используем преобразования Ханкеля и Фурье для решения этой задачи.
Для простоты последующих выкладок запишем уравнение (105) и условия (106) в безразмерной форме
 (108)
(108)
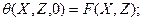 (109)
(109)
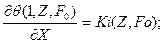 (110)
(110)
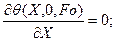
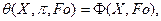 (111)
(111)
где 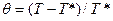 - безразмерная температура (Т* - некоторое начальное значение температуры, фиксированная для определенной точки цилиндра);
- безразмерная температура (Т* - некоторое начальное значение температуры, фиксированная для определенной точки цилиндра); 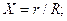
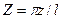 - безразмерные координаты.
- безразмерные координаты.
 ;
; 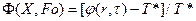 ;
;
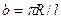 ;
;  ;
;
 .
.
Воспользуемся по переменной Х конечным интегральным преобразованием Ханкеля
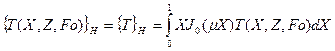 (112)
(112)
и формулой обращения
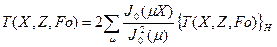 , (113)
, (113)
где 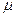 - положительный корень характеристического уравнения
- положительный корень характеристического уравнения 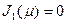 ;
;
а по переменной Z – конечным косинус-преобразованием Фурье
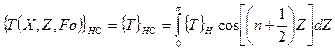 (114)
(114)
и формулой обращения
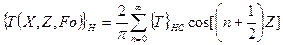 (115)
(115)
Согласно приведенным преобразованиям получим решение задачи в следующем виде

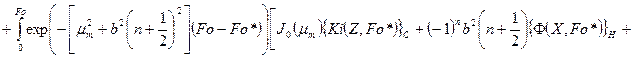

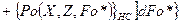 (116)
(116)
Если принять в (115)  и
и 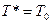 , то найдем
, то найдем

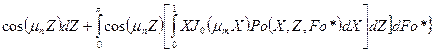 , (117)
, (117)
где 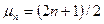 (n=0, 1, 2,…)
(n=0, 1, 2,…)
2). Рассмотрим теперь решение уравнения (106) при выполнении ГУ3 на боковой поверхности цилиндра.
Пусть краевые условия задачи имеют вид
 ;
;
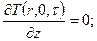
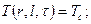
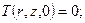
или в безразмерной форме
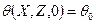 ; (118)
; (118)
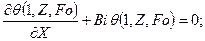 (119)
(119)
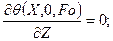
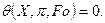 (120)
(120)
В уравнении (108) и условиях (118)-(120) в отличие от предыдущей задачи безразмерный потенциал 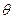 имеет вид
имеет вид
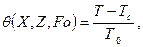
кроме того
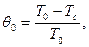
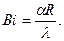
Применяя к уравнению (107) и условиям (117)-(119) последовательно преобразования (111) и (113), найдем обыкновенное неоднородное дифференциальное уравнение в изображениях. Решая его и выполняя обратные интегральные преобразования (115) и (113), после некоторых упрощений получим окончательное решение

 (121)
(121)
где 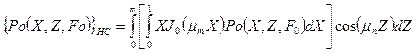 ,
,
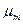 - положительные корни характеристического уравнения
- положительные корни характеристического уравнения
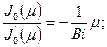
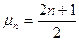 , (n=0, 1, 2,…).
, (n=0, 1, 2,…).
В (121) введено разложение для тета-функции 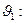

Дата добавления: 2015-08-21; просмотров: 640;
