Сочетания с повторениями. Сочетанием с повторениями из элементов по называется выборка предметов из неограниченного количества предметов различных сортов
Сочетанием с повторениями из  элементов по
элементов по  называется выборка
называется выборка  предметов из неограниченного количества предметов
предметов из неограниченного количества предметов  различных сортов. Такие выборки должны отличаться хотя бы одним элементом, т.е. порядок элементов во внимание не принимается
различных сортов. Такие выборки должны отличаться хотя бы одним элементом, т.е. порядок элементов во внимание не принимается
Число вариантов выбора или количество таких сочетаний обычно обозначается  и вычисляется по формуле
и вычисляется по формуле

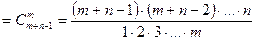 .
.
Каждое сочетание полностью определяется , если указать, сколько элементов каждого из  типов в него входит. Назовем кратностью элемента число повторений данного элемента в сочетании с повторениями. Например, в сочетании
типов в него входит. Назовем кратностью элемента число повторений данного элемента в сочетании с повторениями. Например, в сочетании 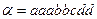 элемент
элемент  имеет кратность
имеет кратность  , элемент
, элемент 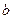 имеет кратность
имеет кратность  , элемент
, элемент 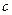 имеет кратность
имеет кратность 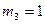 , элемент
, элемент 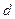 имеет кратность
имеет кратность  . Сумма всех кратностей равна порядку сочетания
. Сумма всех кратностей равна порядку сочетания  , т.е.
, т.е.  . Поставим каждому сочетанию в соответствие последовательность из нулей и единиц, составленную по такому правилу: напишем подряд столько единиц, сколько элементов первого типа в него входит, затем нуль, затем напишем столько единиц, сколько элементов второго типа в него входит, затем нуль и т.д. Например, сочетанию с повторениями
. Поставим каждому сочетанию в соответствие последовательность из нулей и единиц, составленную по такому правилу: напишем подряд столько единиц, сколько элементов первого типа в него входит, затем нуль, затем напишем столько единиц, сколько элементов второго типа в него входит, затем нуль и т.д. Например, сочетанию с повторениями  соответствует последовательность 11101101011. Если некоторый элемент не содержится в данном сочетании с повторениями, т.е. его кратность равна нулю, то тогда группа единиц не пишется и в последовательности появится 0 по меньшей мере два раза. В элементах последовательности из нулей и единиц, соответствующих сочетаниям с повторениями из
соответствует последовательность 11101101011. Если некоторый элемент не содержится в данном сочетании с повторениями, т.е. его кратность равна нулю, то тогда группа единиц не пишется и в последовательности появится 0 по меньшей мере два раза. В элементах последовательности из нулей и единиц, соответствующих сочетаниям с повторениями из  элементов по
элементов по  цифра 1 встречается
цифра 1 встречается  раз, а цифра 0 встречается
раз, а цифра 0 встречается  раз. Для сочетания
раз. Для сочетания  соответственно 8 и 3. Всевозможные сочетания с повторениями получатся, если подвергнуть перестановке нули и единицы в соответствующей последовательности.
соответственно 8 и 3. Всевозможные сочетания с повторениями получатся, если подвергнуть перестановке нули и единицы в соответствующей последовательности.
Каждому сочетанию с повторениями из  элементов по
элементов по  соответствует последовательность из
соответствует последовательность из  единиц и
единиц и  нулей. Следовательно, число сочетаний с повторениями из
нулей. Следовательно, число сочетаний с повторениями из  элементов по
элементов по  равно числу последовательностей из
равно числу последовательностей из  единиц и
единиц и  нулей. Это число определяется числом перестановок с повторениями
нулей. Это число определяется числом перестановок с повторениями  , т.е.
, т.е.  .
.
Например, сочетания из 4-х элементов 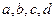 по 2 с повторениями будут
по 2 с повторениями будут 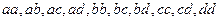 . Им соответствуют следующие последовательности из нулей и единиц
. Им соответствуют следующие последовательности из нулей и единиц
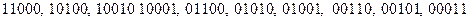

Дата добавления: 2015-08-21; просмотров: 850;
