Сетевые методы

Основные понятия

Сетевое планирование и управление (СПУ) - графоаналитический ме­тод управления процессами создания (проектирования) любых систем.

Сетевой график - это полная графическая модель комплекса работ, направленных на выполнение единого задания, в которой (модели) опре­деляется логическая взаимосвязь, последовательность работ и взаимосвязь между ними.

Элементами сетевого графика являются работа (изображается стрел­кой) и событие (изображается кружком).

Работа- это процесс или действие, которое нужно совершить, чтобы перейти от одного события к другому. Она характеризуется определенны­ми затратами труда и времени. Если для перехода от одного события не требуется ни затрат времени, ни затрат труда, то взаимная связь таких со­бытий изображается пунктирной стрелкой и называется фиктивной рабо­той. Фиктивная работа представляет собой, таким образом, логическую связь между событиями и показывает зависимость начала выполнения ка­кой- либо работы от результатов выполнения другой.

Событие- это фиксированный момент времени, который представ­ляет собой одновременно окончание предыдущей работы, т.е. ее результат (исключение -начальное событие) и начало последующей работы (исключение- конечное событие).

Любая непрерывная последовательность взаимосвязанных событий и работ носит название - ПУТЬ.Путь от начального до конечного события называется полным. Путь от данного события до завершающего называется последующим за данным событием, а от исходного события до данного - предшествующим.

2.4.4.2. При составлении сетевых графиков необходимо выполнять следующие правила:

1. Номер каждого последующего события должен быть больше номе­ра любого предыдущего события. Выполнение этого правила позволяет обеспечить соблюдение логической последовательности выполнения ра­бот.

2. Не должно быть событий, из которых не выходит ни одной работы (исключение- последнее событие). Если данное правило не выполняется, то сетевой график построен неправильно или запланирована лишняя работа (например, "В" на рис. 2.7.).

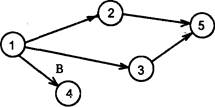
Рис.2.7. Пример неправильного построения сетевого графика с лишней работой "В"

2. Не должно быть событий, в которые не входит не одна работа (исключение - начальное событие). Если данное правило не выполняется, то это означает, что допущена ошибка при построении сетевого графика или не запланирована работа, результат которой (например, событие З на рис. 2.8.) необходим для начала работы "Е".

Рис. 2.8. Пример неправильного построения сетевого графика с лишним со­бытием 5

3. В сетевом графике не должно быть замкнутых контуров, т.к. это приводит к ситуации, когда результатом выполнения последовательности работ (Б-В-Г-Д) является событие 2, с которого началась эта последова­тельность (рис. 2.9.).

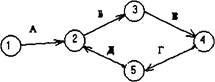
Рис. 2.9. Неправильный сетевой график с замкнутым контуром.

4. Любые два события должны быть соединены не более одной рабо­той. Подобные ошибки являются чаще всего при изображении параллель­но выполняемых работ (рис. 2.10. а). Для правильного изображения этих работ необходимо ввести дополнительные фиктивные события 2' и 2" и фиктивные работы 2' - 2 и 2" - 2 (рис.2.10. б).

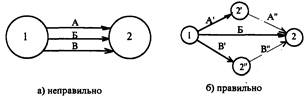
В случае, показанном на рис. 2.10. б, работа "А" представлена как сумма работ А' и А". Фиктивность работ (2' - 2) и (2" - 2) показывает, что для перехода событий 2' и 2"в событие 2 не требуется затрат труда и вре­мени, т.е. события 2' и 2" тождественны событию 2. Подобное изображе­ние дает возможность по-разному обозначить работы А, Б и В, которые на примере "а" имели одинаковую индексацию (1-2).

6. Если какие-либо промежуточные работы сетевого графика могут быть начаты до полного окончания предшествующей работы, то послед­нюю следует разбить на несколько последовательно выполненных работ, каждая из которых достаточна для начала каждой из указанных ранее. Пример неправильного и правильного построения такого сетевого графи­ка представлен на рис. 2.11.

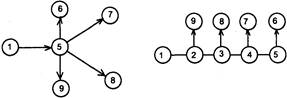
Рис. 2.11. Пример построения графика с несколькими последовательно вы­полненными работами

5. Если для продолжения работы в ее процессе на каких-либо этапах необходимо получить результаты других работ, то следует разделить ука­занную работу на части, используя промежуточные события (в данном примере - событие 4 на рис. 2.12.)

Рис. 2.12. Пример построения графика с входящим промежуточным событием

6. Аналогичные действия необходимо провести и в том случае, если до полного окончания работы нужно видеть промежуточный результат, требующейся до начала другой работы (на рис. 2.13 б работа 2-4)

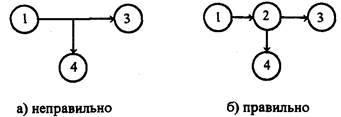
Рис. 2.13. Пример построения графика с выходящим промежуточным собы­тием