Оптимизация сетевых графиков.

Если полученный вариант сетевого графика не обеспечивает выпол­нения комплекса работ в установленные сроки или есть необходимость в максимально возможном сокращении времени окончания последнего, то следует изменить планируемые параметры сетевого графика, т.е. провести оптимизацию. Кроме того, в связи с ограниченностью ресурсов (трудовых, материальных и др.) возникает вопрос о таком их распределении, при ко­тором за время выполнения разработки затраты были бы минимальны.

В данном случае рассматривается оптимизация сроков выполнения комплекса работ. Для решения этой задачи необходимо перераспределение имеющихся или привлечение дополнительных ресурсов.

Так как время выполнения всего комплекса работ определяет про­должительности критического пути, то объектом оптимизации должны быть работы критического пути.Вместе с тем, объектом оптимиза­ции могут быть и работы путей, которые близки по своей продолжитель­ности критическому и случае уменьшения последнего могут образовать новый критический путь.

Работы критического и подкритического путей образуют крити­ческую зону. Коэффициент напряженности для этих работ составляет

0.85 £Кщ<1.

Оптимизация сроков выполнения за счет перераспределения ресурсов основана на том, что работы, не лежащие на критическом пути, имеют ре­зервы времени. Для переброски ресурсов, например, людей, используются работы с коэффициентом напряженности в интервале от 0 до 0.55, что определяет принадлежность работ к зоне резерва.

Уравнения оптимизации выглядят следующим образом: а) для ij-йработы, не принадлежащей критическому пути, с которой перебрасывают ресурсы

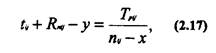
где у - время, на которое сократится продолжительность критического пути при переброске ресурсов;

х - количество ресурсов (человек), которое переводится на работу критического пути.

- это время выполнения ij - и работы, при котором она образует новый критический путь, т.е. в этом случае она тождественна mk - и работе критического пути. б) для rak - и работы, принадлежащей критическому пути

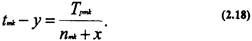
Решая систему уравнений (2.17) и (2.18) найдем х и у. После этого необхо­димо сравнить новое полученное значение критического пути с макси­мальным значением подкритического пути с целью установления, не стал ли последний критическим. В случае необходимости процесс оптимизации может быть продолжен.

2.4.4.6. Пример.Рассчитать графическим методом параметры следующего сетевого графика.

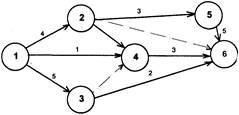
Решение.

В соответствии с изложенными выше требованиями расчет произво­дится непосредственно на графике. Рекомендуется следующая последова­тельность действий.