Случай связных выборок

В случае связанных выборок с равным числом измерений в каждой можно использовать более простую формулу t-критерия Стьюдента.

Вычисление значения t_эмп осуществляется по формуле:

где

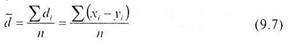
где 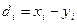- разности между соответствующими значениями переменной X ипеременной Y, а 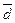среднее этих разностей.

В свою очередь Sd вычисляется по следующей формуле:

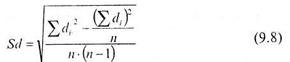
Число степеней свободы к определяется по формуле k = n - 1. Рассмотрим пример использования t - критерия Стьюдента для связных, равных по численности выборок.

Задача 9.2.Психолог предположил, что в результате научения время решения эквивалентных задач «игры в 5» (т.е. имеющих один и тот же алгоритм решения) будет значимо уменьшаться. Для проверки гипо­тезы у восьми испытуемых сравнивалось время решения (в минутах) первой и третьей задач.

Решение. Решение задачи представим в виде таблицы 9.2:

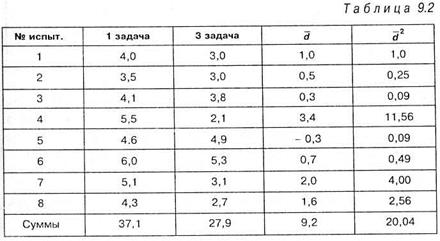
Вначале произведем расчет по формуле (9.7):

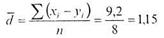
Затем применим формулу (9.8), получим:

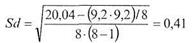
И, наконец, следует применить формулу (9.6). Получим:

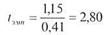
Число степеней свободы: k = 8 – 1 = 7 и по таблице 16 При­ложения 1 находим t_кр :

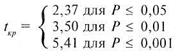
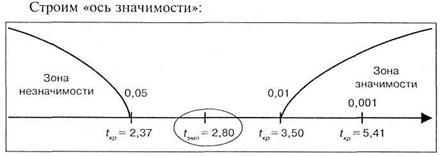
Таким образом, на 5% уровне значимости первоначальное предположение подтвердилось, действительно, среднее вре­мя решения третьей задачи существенно меньше среднего времени решения первой задачи. В терминах статистических гипотез полученный результат будет звучать так: на 5% уров­не гипотеза Н₀ отклоняется и принимается гипотеза Н₁ — о различиях.

Для применения t-критерия Стъюдента необходимо соблюдать следующие условия:

1. Измерение может быть проведено в шкале интервалов и отно­шений.

2. Сравниваемые выборки должны быть распределены по нор­мальному закону.