Сравнение двух выборок по качественно определенному признаку

Задача 8.14.Психолог провел эксперимент, в котором выяс­нилось, что из 23 учащихся математической спецшколы 15 справились с заданием, а из 28 обычной школы с тем же заданием справились 11 человек. Можно ли считать, что различия в ус­пешности решения заданий учащимися спец­школы и обычной школы достоверны?

Решение. Для решения этой задачи с помощью критерия Фишера показатели успешности выполнения за­даний необходимо перевести в проценты. В про­центах это составит:

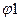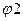По таблице 14 Приложения 1 находим величины и соответствующие процентным долям в каждой группе. Так для 65,2% согласно таблице соответствующая величина 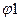=1,880, а для 39,3% величина 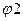= 1,355.

Эмпирическое значение 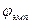подсчитывается по формуле:

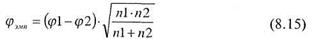
Где 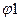- величина, взятая из таблицы 14 Приложения 1, соот­ветствующая большей процентной доле;

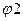- величина, взятая из таблицы 14 Приложения 1, соот­ветствующая меньшей процентной доле;

п1—количество наблюдений в выборке 1;

п2— количество наблюдений в выборке 2.

В нашем случае

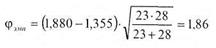
По таблице 15 Приложения 1 определяем, какому уровню значимости соответствует

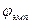= 1,86.

С таблицей 15 Приложения 1 работают следующим образом: на­ходят внутри ее число равное вычисленному 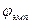, и смотрят, между какими уровнями значимости (с учетом тысячной доли) оно нахо­дится. Следовательно, уровень зна­чимости 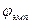= 1,86 равен 0,03 + 0,001 = 0,031.

Следует подчеркнуть, однако, что поскольку критические значения для 5% и 1% уровней значимости имеют фиксирован­ную величину и составляют соответственно для 5% 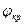= 1,64, а для 1% 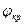= 2,28, то таблица 15 Приложения 1 практически не нужна, так как вышеозначенными величинами критических уровней можно пользоваться всегда. В привычной форме записи, это выглядит так:

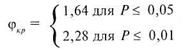
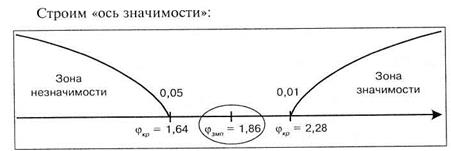
Поскольку мы попали в зону неопределенности, то в терми­нах статистических гипотез в данном примере можно принять гипотезу Н₁ на 5% уровне значимости и отклонить ее на 1% уровне значимости. Иными словами, на 5% уровне значимости можно говорить о различии между успешностью в решении заданий учениками сравниваемых школ, а на уровне в 1% — этого утверждать нельзя.