Сравнение двух выборок по количественно определенному признаку

Критерий Фишера с равным успехом может использоваться и при сравнении распределений количественных признаков.

Задача 8.15.Будет ли уровень тревожности у подростков-сирот более высоким, чем у их сверстников из полных семей? Для решения этой задачи психолог про­водил анализ выраженности уровня тревожности в группе сирот и в группе детей из полных семей при помощи опросника Тейлора. 40 баллов и выше рассматривались как показатель очень вы­сокого уровня тревоги (

Решение. В первой группе из 10 человек очень высокий уро­вень тревожности наблюдался у 7 испытуемых (70%), во второй группе из 13 человек он был обнаружен у 3 испытуемых (23,1%). Проверим, можно ли считать подобные различия статисти­чески значимыми?

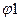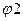По таблице 14 Приложения 1 определяем величины и для первой и второй группы:

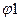=1,982 для 70% и 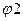= 1,003 для 23,1%.

Подсчитываем 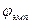по формуле (8.14):

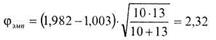
Напомним, что критические величины для этого критерия таковы:

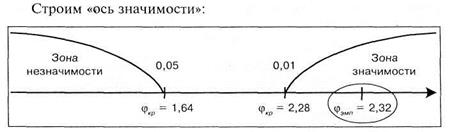
Полученная величина 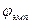превышает соответствующее кри­тическое значение для уровня в 1%, следовательно, различия между группами значимы на 1% уровне. Иными словами в пер­вой группе измеряемый признак выражен в существенно боль­шей степени, чем во второй.

Т.е. подростки сироты более тревожны, чем дети из полных семей. Обратите внимание, что для получения подобного вывода понадобилась очень малая выборка испытуемых.

В терминах статистических гипотез можно утверждать, что нулевая гипотеза Н₀ отклоняется и на высоком уровне значимо­сти принимается гипотеза Н₁ о различиях.

Как уже говорилось ранее, критерии носят название «параметрические», потому что в формулу их расчета включаются такие параметры выборки, как среднее, дисперсия и др. Как правило, в психологических иссле­дованиях чаще всего применяются два параметрических крите­рия — это t - критерий Стьюдента, который оценивает различия средних для двух выборок и F - критерий Фишера, оцениваю­щий различия между двумя дисперсиями.