Замечание 2
Если в формуле (1.2.9) окажется, что 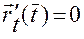 при каких-то значениях
при каких-то значениях  , то подбираем новую параметризацию
, то подбираем новую параметризацию 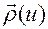 , в которой параметр
, в которой параметр 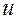 связан со временем
связан со временем 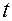 соотношением
соотношением
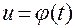 , (1.2.11)
, (1.2.11)
допускающим однозначное и дважды непрерывно дифференцируемое обращение 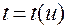 .
.
Основное требование к указанной параметризации следующее:
-вектор-функция 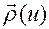 , определяемая по формуле
, определяемая по формуле
 (1.2.12)
(1.2.12)
должна иметь значение
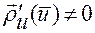 при
при 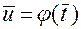 .
.
Поскольку траектория движения 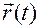 является регулярной кривой без особых точек, то такая параметризация
является регулярной кривой без особых точек, то такая параметризация 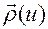 существует.
существует.
Данное утверждение следует из того, что для регулярных кривых без особых точек всегда существует естественная параметризация 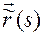 . А в естественной параметризации при всех значениях длины дуги
. А в естественной параметризации при всех значениях длины дуги 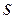 выполняется равенство
выполняется равенство
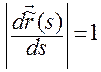 .
.
После построения параметризации 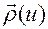 траектория с учетом соотношения (1.2.12) будет задаваться равенством
траектория с учетом соотношения (1.2.12) будет задаваться равенством
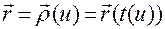 (1.2.13)
(1.2.13)
А тогда функцию 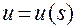 находим путем обращения функции
находим путем обращения функции 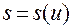 , где
, где 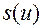 имеет следующую зависимость от функции
имеет следующую зависимость от функции 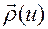 :
:
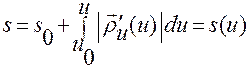 . (1.2.14)
. (1.2.14)
Соотношение (1.2.14) выводится по той же схеме, по которой получено (1.2.9):
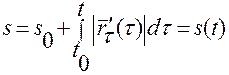 ,
, 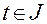 (1.2.9)
(1.2.9)
Это делается путем замены 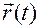 на
на 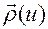 .
.
Так как функция 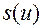 , определяемая по формуле (1.2.14), обладает свойством
, определяемая по формуле (1.2.14), обладает свойством
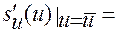
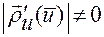 ,
,
то в окрестности точки 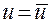 ,
, 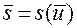 она допускает обращение
она допускает обращение
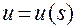 .
.
Подстановка вместо 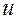 :
:
1) функции 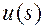 в соотношение (1.2.13)
в соотношение (1.2.13)
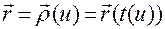 , (1.2.13)
, (1.2.13)
2) функции 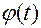 из (1.2.11)
из (1.2.11)
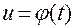 , (1.2.11)
, (1.2.11)
в функцию 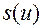 , определяемую по формуле (1.2.14)
, определяемую по формуле (1.2.14)
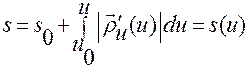 , (1.2.14)
, (1.2.14)
дает окончательно естественный способ задания движения:
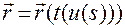 ,
, 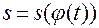 .
.
Дата добавления: 2015-08-21; просмотров: 871;
