Определение 15
Если существует предел 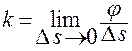 , то он называется кривизной кривой
, то он называется кривизной кривой 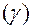 в точке
в точке 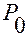 .
.
Очевидно, кривизна 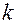 кривой
кривой 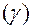 всегда неотрицательна, т.е.
всегда неотрицательна, т.е. 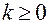 .
.
В дифференциальной геометрии доказано, что если кривая задается в параметризации 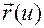 , то в любой неособой точке, где существуют
, то в любой неособой точке, где существуют 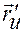 и
и 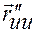 , кривизна кривой может быть вычислена по формуле
, кривизна кривой может быть вычислена по формуле
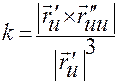 .
.
Если кривая задается в естественной параметризации, то
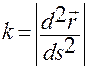 .
.
Дата добавления: 2015-08-21; просмотров: 832;
