Практические задачи на экстремум.

Задача 1. Каковы должны быть размеры (радиус основания R и высота H) открытого сверху цилиндрического бака максимальной вместимостью, если для его изготовления отпущено 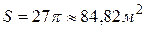материала?

Решение. Вместимость бака 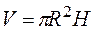, а на его изготовление пойдет материала площадью .

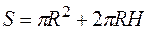Отсюда определяем высоту бака .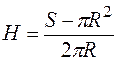

Тогда вместимость бака .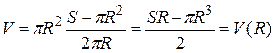

Найдем то значение R, при котором вместимость V(R) будет максимальной. Имеем:

.

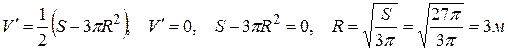Так как 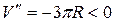, то при найденном значении R = 3 вместимость бака будет максимальной.

Высота бака находится из полученного выше соотношения:

.

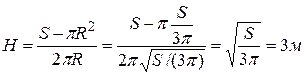Ответ: R = 3м, H = 3м.

Задача 2.Сечение оросительного канала имеет форму равнобочной трапеции, боковые стороны которой равны меньшему основанию. При каком угле наклона a боковых сторон этой трапеции сечение канала будет иметь наибольшую площадь?

Решение. Определим площадь сечения канала как функцию угла a, считая, что боковые стороны и меньшее основание трапеции равны .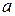

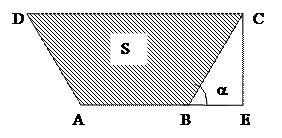
Тогда, как видно из рисунка

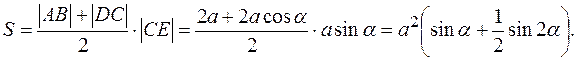
Исследуем S как функцию аргумента a на экстремум.

Имеем:

.

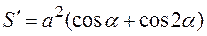В критических точках

.

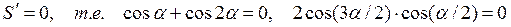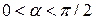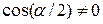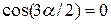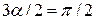Так как , то . Поэтому, если , то или .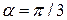

Докажем, что при 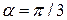функция S достигает наибольшего значения на отрезке 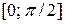. Действительно,

.

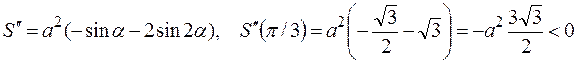Поэтому при 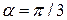имеем локальный максимум 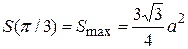, который на отрезке 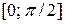будет также наибольшим значением функции S, поскольку S(0) = 0, S(p/2) = a² < S_max.

Задача 3.Известно, что прочность бруса с прямоугольным поперечным сечением пропорциональна его ширине 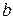и квадрату высоты 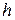. Найти размеры бруса наибольшей прочности, который можно вырезать из бревна радиусом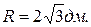

Решение.Прочность бруса N, вычисляется по формул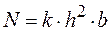е , где 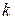- коэффициент пропорциональность, 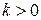. Из рисунка видно, что 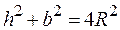, т.е.

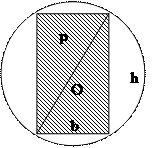
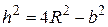. Тогда

.

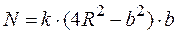Найдем экстремум функции

:

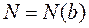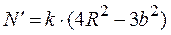. Если 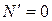, то

.

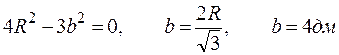Тогда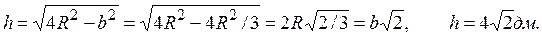

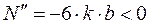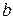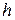Так как , то при найденных значениях и прочность бруса будет максимальной.