Дифференциал длины дуги и кривизна плоской линии.
Дифференциал ds длины дуги s плоской линии, заданной уравнением y = f(x), выражается формулой
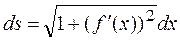 .
.
Если линия задана уравнением 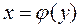 , то
, то 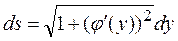 .
.
В случае параметрического задания линии уравнениями 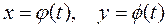
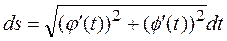 .
.
Если линия задана в полярной системе координат уравнением 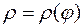
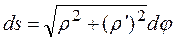 .
.
Задача 4. Найти дифференциал длины дуги циклоиды, заданной уравнениями: 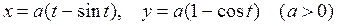 .
.
Решение. Имеем: 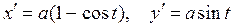 . Тогда
. Тогда
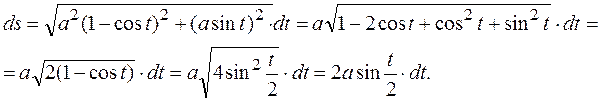 .
.
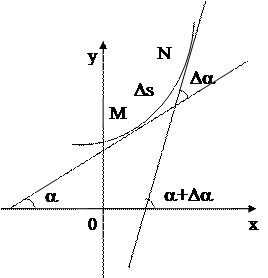 Определение 1. Кривизной К любой плоской линии в точке М называется предел модуля отношения угла между положительными направлениями касательных в точках М и N линии (угла смежности) к длине дуги
Определение 1. Кривизной К любой плоской линии в точке М называется предел модуля отношения угла между положительными направлениями касательных в точках М и N линии (угла смежности) к длине дуги  , когда
, когда 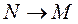 , т.е. по определению
, т.е. по определению
, 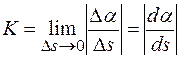
где a - угол наклона
касательной в точке
М к оси Ох.
Определение 2. Радиусом кривизныназывается величина R, обратная кривизне Клини, т.е. 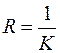 . Например, для окружности
. Например, для окружности 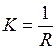 , где R – радиус окружности; для прямой К = 0. Для произвольной линии кривизна не является величиной постоянной.
, где R – радиус окружности; для прямой К = 0. Для произвольной линии кривизна не является величиной постоянной.
Если линия задана уравнением y = f(x), то кривизна в любой ее точке вычисляется по формуле
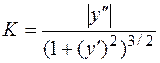 .
.
В случае параметрического задания линии уравнениями 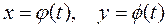 для вычисления кривизны применяется формула
для вычисления кривизны применяется формула
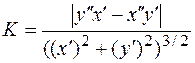 , где производные берутся по переменной t.
, где производные берутся по переменной t.
Если линия задана в полярной системе координат уравнением 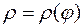 , то
, то
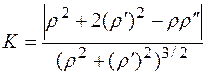 .
.
Задача 5. Найти кривизну и радиус кривизны линии 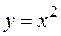 в точке М(1; 1).
в точке М(1; 1).
Вычислим значения первой и второй производных данной функции в точке М: 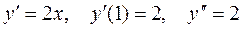 . Тогда
. Тогда 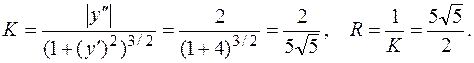
Дата добавления: 2015-08-21; просмотров: 2693;
