Наибольшее и наименьшее значения функции на отрезке
Одной из важнейших прикладных задач дифференциального исчисления является разработка общих приемов исследования поведения функций.
Определение 1 Функция 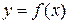 называется возрастающей (убывающей) в некотором интервале, если большему значению аргумента из этого интервала соответствует большее (меньшее) значение функции, т.е. при
называется возрастающей (убывающей) в некотором интервале, если большему значению аргумента из этого интервала соответствует большее (меньшее) значение функции, т.е. при 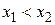 выполняется неравенство
выполняется неравенство 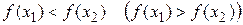 .
.
Перечислим признаки возрастания (убывания) функции.
1. Если дифференцируемая функция 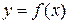 на отрезке
на отрезке 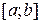 возрастает (убывает), то ее производная на этом отрезке неотрицательна (неположительная), т.е.
возрастает (убывает), то ее производная на этом отрезке неотрицательна (неположительная), т.е. 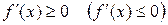 .
.
2. Если непрерывная на отрезке 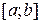 и дифференцируемая внутри него функция имеет положительную (отрицательную) производную, то она возрастает (убывает) на этом отрезке.
и дифференцируемая внутри него функция имеет положительную (отрицательную) производную, то она возрастает (убывает) на этом отрезке.
Определение 2 Функция 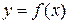 называется неубывающей (невозрастающей) в некотором интервале, если для любых
называется неубывающей (невозрастающей) в некотором интервале, если для любых 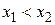 из этого интервала выполняется неравенство
из этого интервала выполняется неравенство 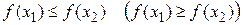 .
.
Определение 3 Точки, в которых первая производная функции обращается в нуль, называются стационарными. Точки, в которых первая производная функции обращается в нуль или терпит разрыв, называются критическими.
Пример 1. Найти интервалы монотонности (возрастания и убывания) и критические точки функции 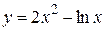 .
.
Решение. Данная функция определена при x > 0. Находим ее производную: 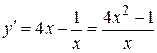 . Из условия
. Из условия 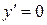 , найдем стационарные точки.
, найдем стационарные точки. 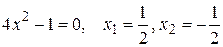 . Эти точки разбивают область определения функции на интервалы
. Эти точки разбивают область определения функции на интервалы 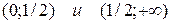 . В первом из них
. В первом из них 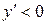 , а во втором
, а во втором 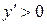 . Это означает, что в интервале (0; 0,5) данная функция убывает, а в интервале (0,5; +¥) – возрастает.
. Это означает, что в интервале (0; 0,5) данная функция убывает, а в интервале (0,5; +¥) – возрастает.
Определение 4 Точка х1 называется точкой локального максимума функции 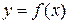 , если для любых достаточно малых
, если для любых достаточно малых 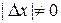 выполняется неравенство
выполняется неравенство  .
.
Определение 5 Точка х2 называется точкой локального минимума функции 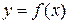 , если для любых достаточно малых
, если для любых достаточно малых 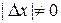 выполняется неравенство
выполняется неравенство 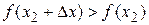 .
.
Определение 6 Точка максимума и минимума называется точками экстремума функции, а максимумы и минимумы функции ее экстремальными значениями.
Теорема 1(необходимый признак локального экстремума)
Если функция 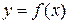 имеет в точке х = х0 экстремум, то либо
имеет в точке х = х0 экстремум, то либо 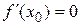 , либо
, либо 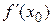 не существует.
не существует.
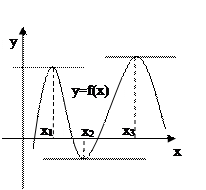 Эта теорема имеет следующий геометрический смысл. Если х1, х2 и х3 – точки локального экстремума и в соответствующих точках графика существуют касательные, то эти касательные параллельны оси Ох. Эти точки и называются стационарными точками; мы будем называть их точками возможного экстремума.
Эта теорема имеет следующий геометрический смысл. Если х1, х2 и х3 – точки локального экстремума и в соответствующих точках графика существуют касательные, то эти касательные параллельны оси Ох. Эти точки и называются стационарными точками; мы будем называть их точками возможного экстремума.
Если точка х0 – точка возможного экстремума, т.е. 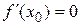 , то она может и не быть точкой локального максимума или минимума. Например, если
, то она может и не быть точкой локального максимума или минимума. Например, если 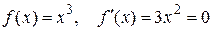 при
при 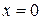 , но, тем не менее, в точке х = 0 нет локального экстремума. Установим достаточное условие существования локального экстремума.
, но, тем не менее, в точке х = 0 нет локального экстремума. Установим достаточное условие существования локального экстремума.
Теорема 2(первый достаточный признак локального экстремума)
Пусть функция 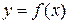 непрерывна в некотором интервале, содержащем критическую точку х = х0, и дифференцируема во всех точках этого интервала (кроме, быть может, самой точки х0). Если
непрерывна в некотором интервале, содержащем критическую точку х = х0, и дифференцируема во всех точках этого интервала (кроме, быть может, самой точки х0). Если 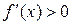 при
при 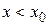 , а при
, а при 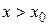 производная
производная 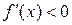 , то при х = х0 функция
, то при х = х0 функция 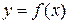 имеет максимум. Если же
имеет максимум. Если же 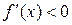 при
при 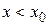 , а при
, а при 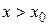
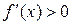 , то при х = х0 данная функция имеет минимум.
, то при х = х0 данная функция имеет минимум.
Схема исследования функции 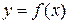 на экстремум с помощью первой производной может быть записана в виде таблицы.
на экстремум с помощью первой производной может быть записана в виде таблицы.
| Числовые промежутки | (-∞; x0) | x0 | (x0; +∞) |
Знаки производной: 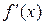
| + | - | |
Поведение функции: 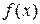
| 
| 
| 
|
Пример 2. Исследовать на экстремум функцию 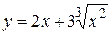 .
.
Решение. 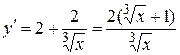 . Из условия
. Из условия 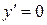 , находим критические точки х1 = -1 и х2 = 0 (точка разрыва).
, находим критические точки х1 = -1 и х2 = 0 (точка разрыва).
| Числовые промежутки | (-∞; -1) | -1 | (-1; 0) | (0; +∞) | |
Знаки производной: 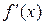
| + | - | + | ||
Поведение функции: 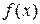
| 
| - | 
| - | 
|
Значит точка х = -1 является точкой локального максимума, а точка х = 0 – точка локального минимума.
Теорема 3(второй достаточный признак локального экстремума функции)
Пусть функция 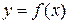 дважды дифференцируема и
дважды дифференцируема и 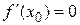 . Тогда в точке х = х0 функция имеет локальный максимум, если
. Тогда в точке х = х0 функция имеет локальный максимум, если 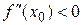 , и локальный минимум, если
, и локальный минимум, если 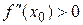 .
.
В случае, когда 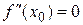 , точка х = х0 может и не быть экстремальной.
, точка х = х0 может и не быть экстремальной.
Пример 3. С помощью второй производной исследовать на экстремум функцию 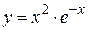 .
.
Решение.

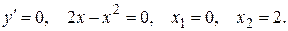
Вычисляем значения второй производной в этих точках: 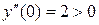 , т.е. х1 = 0 – точка минимума;
, т.е. х1 = 0 – точка минимума; 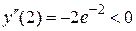 , т.е. х2 = 2 – точка максимума;
, т.е. х2 = 2 – точка максимума;
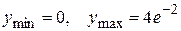 .
.
На отрезке 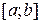 функция
функция 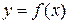 может достигать наименьшего
может достигать наименьшего 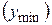 или наибольшего
или наибольшего 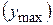 значения либо в критических точках функции, лежащих в интервале
значения либо в критических точках функции, лежащих в интервале 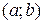 , либо на концах отрезка
, либо на концах отрезка 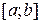 .
.
Пример 4. Найти наименьшее и наибольшее значения функции 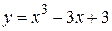 на отрезке
на отрезке 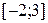 .
.
Решение. 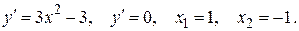 Обе эти точки принадлежат интервалу (-2;3). Вычислим значения функции в критических точках и на концах отрезках: у(-1) = 5, у(1) = 1, у(-2) = 1, у(3) = 21. Сравнивая полученные числа, получаем наименьшее значение в точках х1= 1 и х2 = -2, а наибольшее значение – в точке х3 = 3. Значит
Обе эти точки принадлежат интервалу (-2;3). Вычислим значения функции в критических точках и на концах отрезках: у(-1) = 5, у(1) = 1, у(-2) = 1, у(3) = 21. Сравнивая полученные числа, получаем наименьшее значение в точках х1= 1 и х2 = -2, а наибольшее значение – в точке х3 = 3. Значит 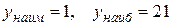 .
.
Определение 7 Кривая, заданная функцией 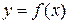 , называется выпуклой в интервале (а;b), если все точки кривой лежат не выше любой ее касательной в этом интервале, и вогнутой в интервале (a;b), если все ее точки лежат не ниже любой ее касательной в этом интервале.
, называется выпуклой в интервале (а;b), если все точки кривой лежат не выше любой ее касательной в этом интервале, и вогнутой в интервале (a;b), если все ее точки лежат не ниже любой ее касательной в этом интервале.
Определение 8 Точка кривой 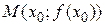 , отделяющая выпуклую ее часть от вогнутой, называется точкой перегиба кривой. Предполагается, что в точке М существует касательная.
, отделяющая выпуклую ее часть от вогнутой, называется точкой перегиба кривой. Предполагается, что в точке М существует касательная.
Теорема 4(достаточное условие выпуклости (вогнутости) графика функции)
Если во всех точках интервала 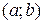 вторая производная функции
вторая производная функции 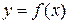 отрицательна (положительна), т.е.
отрицательна (положительна), т.е. 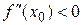
 , то кривая
, то кривая 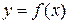 в этом интервале выпукла (вогнута).
в этом интервале выпукла (вогнута).
В точке перегиба, отделяющей промежуток выпуклости от промежутка вогнутости, вторая производная функции изменяет свой знак, поэтому в таких точках вторая производная функции или обращается в нуль, или не существует.
Теорема 5(достаточный признак точки перегиба)
Если в точке х = х0 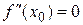 или
или 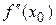 не существует и при переходе через эту точку производная
не существует и при переходе через эту точку производная 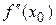 меняет знак, то точка с абсциссой х = х0 кривой
меняет знак, то точка с абсциссой х = х0 кривой 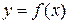 - точка перегиба.
- точка перегиба.
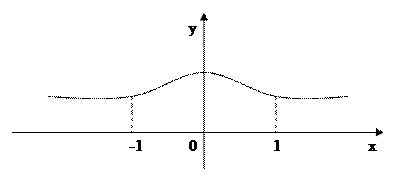
Пример 5. Найти точки перегиба, интервалы выпуклости и вогнутости кривой 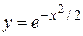 (кривая Гаусса).
(кривая Гаусса).
Решение. Находим первую и вторую производные:
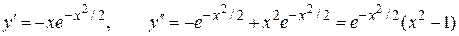 .
.
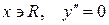 следовательно
следовательно 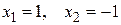 .
.
| Числовые промежутки | (-∞; -1) | -1 | (-1; 0) | (0; 1) | (1; +∞) | ||
Знаки производной: 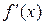
| + | + | - | - | |||
Поведение функции: 
| 
| - | 
| - | 
| 
| |
Знаки второй производной: 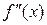
| + | - | - | + | |||
Поведение функции: 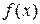
| 
| 
| 
| 
|
х = -1, х = 1 точки перегиба.
Дата добавления: 2015-08-21; просмотров: 1600;
