Оценка остаточного члена для произвольной функции.
Оценим для произвольной функции остаточный член в формуле Макларена, взятый в форме Лагранжа.
.
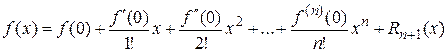Остаточный член в форме Лагранжа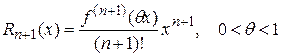 
.
Предположим, что рассматриваемая нами функция f(x) обладает следующим свойством: существует такое вещественное число М, что для всех номеров n и для всех значений аргумента х из рассматриваемой окрестности точки х = 0 справедливо неравенство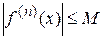 
.
Такую функцию будем называть функцией, совокупность всех производных которой ограничена в окрестности точки х = 0.
Их неравенства вытекает, что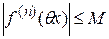 
, и поэтому из формулы остаточного члена следует, что 
.
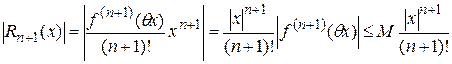Итак, мы получаем следующую универсальную оценку остаточного члена для функции, совокупность всех произвольных которой ограничена числом М в окрестности точки х = 0:
.
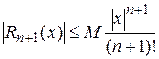Дата добавления: 2015-08-21; просмотров: 1078;