Глава 7. Краевые задачи оптимального управления………………..226 8 страница

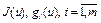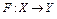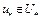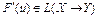Теорема 6. Пусть функционалы , оператор непрерывны и дифференцируемы по Фреше в окрестности точки , множество . Пусть, кроме того, оператор непрерывен в точке 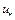и образ пространства X при отображении замкнут. Тогда существуют не равные одновременно нулю множители Лагранжа 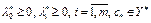такие, что

.

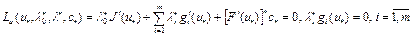Если, кроме того, 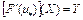, т.е. 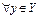, найдется такой, что 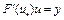, и существует точка 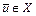такая, что 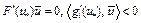для индексов i, для которых 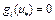, то .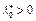

Рекомендуемая литература: Алексеев В. М., Тихомиров В. М., Фомин С. В. Оптимальное управление. – М.: Наука, 1979.

ЛЕКЦИЯ 10.СВОЙСТВА ВЫПУКЛЫХ МНОЖЕСТВ И ВЫПУКЛЫХ ФУНКЦИОНАЛОВ

Рассмотрим задачу оптимального управления: минимизировать функционал

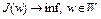
на множестве W банахова пространства X. В лекции 5 была доказана теорема Вейерштрасса для случая, когда W – слабо бикомпактное множество, слабо полунепрерывный снизу функционал на W. Целесообразно иметь легко проверяемые условия слабой бикомпактности множества W и слабой полунепрерывности снизу функционала .