Глава 7. Краевые задачи оптимального управления………………..226 4 страница
б) покажем, что оператор Ф(x) является сжимающим в 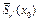 . Как следует из леммы 1 (лекция 2), для этого достаточно показать, что
. Как следует из леммы 1 (лекция 2), для этого достаточно показать, что 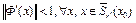 . В самом деле,
. В самом деле,
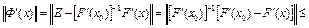
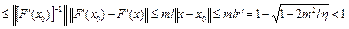 ,
, 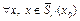 , E – единичный оператор.
, E – единичный оператор.
Итак, оператор Ф(x) отображает 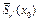 в себя и
в себя и 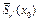 является сжимающим. Тогда согласно теореме 1 (лекция 3) оператор Ф(x) имеет единственную неподвижную точку
является сжимающим. Тогда согласно теореме 1 (лекция 3) оператор Ф(x) имеет единственную неподвижную точку  в
в 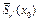 и последовательность
и последовательность 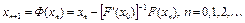 сходится к точке
сходится к точке  . Так как
. Так как
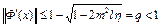 ,
,
то оценка скорости сходимости следует из формулы (1) (лекция 3), где 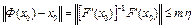 . Тогда
. Тогда
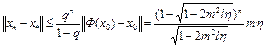 .
.
Теорема доказана.
Пример. Рассмотрим краевую задачу для обыкновенного дифференциального уравнения следующего вида
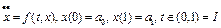 , (13) где функция
, (13) где функция 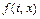 непрерывно дифференцируема при
непрерывно дифференцируема при  .
.
а) приведение краевой задачи (13) к функциональному уравнению вида F(x)=0. Пусть банахово пространство 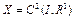 , банахово пространство
, банахово пространство 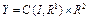 с нормами
с нормами 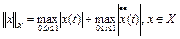 ,
, 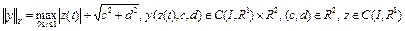 . Оператор
. Оператор 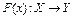 определим следующим образом
определим следующим образом
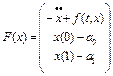 . (14)
. (14)
Теперь краевая задача (13) запишется в виде F(x)=0.
б) вычислим производную Фреше оператора F(x). Так как
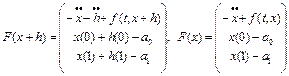 ,
,
то разность
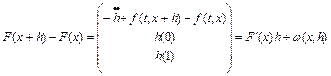 .
.
Поскольку функция f(t,x) непрерывно дифференцируема, то 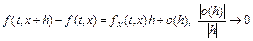 при
при 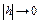 . Тогда
. Тогда
 .
.
Отсюда следует, что
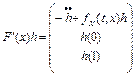 . (15)
. (15)
в) строим итерационный процесс Ньютона-Канторовича по формуле (1). Из (1) следует, что
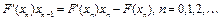 . (16)
. (16)
Как следует из формул (14), (15):
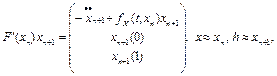
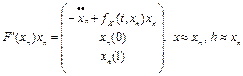 ,
,
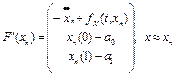 .
.
Теперь итерационный процесс Ньютона-Канторовича (16) запишется так:
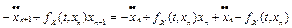 ,
,
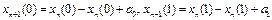 .
.
Отсюда имеем
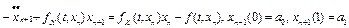 , (17) где
, (17) где 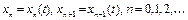 . Таким образом, исходная нелинейная краевая задача (13) сведена к решению последовательности линейных краевых задач.
. Таким образом, исходная нелинейная краевая задача (13) сведена к решению последовательности линейных краевых задач.
Пусть 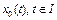 – начальное приближение. Тогда
– начальное приближение. Тогда
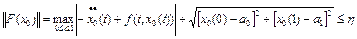 .
.
Элементы открытого шара 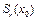 удовлетворяют условию
удовлетворяют условию
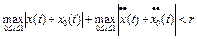 .
.
Если функция 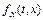 удовлетворяет условию
удовлетворяет условию
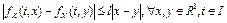 ,
,
то оператор 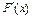 удовлетворяет условию Липшица. Действительно, из (15) имеем
удовлетворяет условию Липшица. Действительно, из (15) имеем
 .
.
Тогда
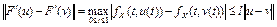 .
.
Рекомендуемая литература: Канторович Л. В., Акилов Г. П. Функцио-нальный анализ. –М.: Наука, 1984;
Треногин В. А. Функциональный анализ. –М.: Наука, 1986.
ЛЕКЦИЯ 5.ТЕОРЕМА ВЕЙЕРШТРАССА В БАНАХОВОМ ПРОСТРАНСТВЕ
Приведены классические теоремы Вейерштрасса о достижении нижней грани функционала на заданном множестве банахова пространства.
Бикомпактные множества и теорема Вейерштрасса. Рассмотрим задачу оптимального управления (см. (9), лекция 1)
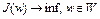 , (1) где W – заданное множество в банаховом пространстве,
, (1) где W – заданное множество в банаховом пространстве,  – функционал, определенный на множестве W. Теоремами Вейерштрасса назовем утверждения о достижении нижней грани функционала на заданном множестве.
– функционал, определенный на множестве W. Теоремами Вейерштрасса назовем утверждения о достижении нижней грани функционала на заданном множестве.
В бесконечномерном пространстве теорема Больцано-Вейерштрасса, в общем случае, неверна. В самом деле, ортонормированная система 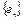 в гильбертовом пространстве H ограничена, однако сама последовательность и любая ее подпоследовательность не сходятся.
в гильбертовом пространстве H ограничена, однако сама последовательность и любая ее подпоследовательность не сходятся.
Определение 1. Множество W банахова пространства X называется бикомпактным, если из любой подпоследовательности 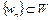 можно выделить хотя бы одну подпоследовательность
можно выделить хотя бы одну подпоследовательность 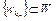 , которая сходится к некоторой точке w, причем
, которая сходится к некоторой точке w, причем  .
.
Легко убедиться в том, что бикомпактное множество W банахова пространства X ограничено и замкнуто. Бикомпактное множество представляет случай, когда верна теорема Больцано-Вейерштрасса.
Теорема 1. Пусть  – непрерывный функционал, определенный на бикомпактном множестве W банахова пространства X. Тогда функционал
– непрерывный функционал, определенный на бикомпактном множестве W банахова пространства X. Тогда функционал  ограничен как сверху, так и снизу на множестве W.
ограничен как сверху, так и снизу на множестве W.
Доказательство. Покажем, что непрерывный функционал  ограничен сверху на бикомпактном множестве W, т.е. существует конечное число c такое, что
ограничен сверху на бикомпактном множестве W, т.е. существует конечное число c такое, что 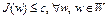 .
.
Предположим противное, т.е. функционал  не ограничен сверху на W. Тогда найдутся элементы
не ограничен сверху на W. Тогда найдутся элементы 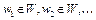 , такие, что
, такие, что 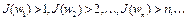 . Следовательно, существует последовательность
. Следовательно, существует последовательность 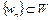 такая, что
такая, что 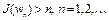 . Так как множество W бикомпактно, то найдется подпоследовательность
. Так как множество W бикомпактно, то найдется подпоследовательность 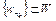 такая, что
такая, что 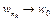 при
при 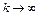 ,
, 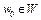 . Тогда в силу непрерывности функционала
. Тогда в силу непрерывности функционала  имеем
имеем 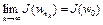 . Отсюда следует, что числовая последовательность
. Отсюда следует, что числовая последовательность 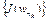 ограничена. Это противоречит тому, что
ограничена. Это противоречит тому, что  при
при 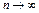 . Аналогичным путем можно доказать ограниченность снизу функционала
. Аналогичным путем можно доказать ограниченность снизу функционала  на W. Теорема доказана.
на W. Теорема доказана.
Теорема 2. Пусть  – непрерывный функционал, определенный на бикомпактном множестве W банахова пространства X. Тогда
– непрерывный функционал, определенный на бикомпактном множестве W банахова пространства X. Тогда
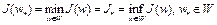 , (2)
, (2)
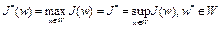 . (3)
. (3)
Доказательство. Пусть 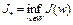 . Докажем, что нижняя грань функционала
. Докажем, что нижняя грань функционала  достигается в точке
достигается в точке 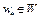 , т.е.
, т.е. 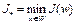 . Из определения нижней грани следует, что для любого
. Из определения нижней грани следует, что для любого 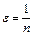 существует точка
существует точка 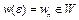 такая, что
такая, что 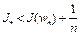 . Отсюда следует, что
. Отсюда следует, что 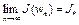 .
.
Последовательность 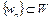 , следовательно, существует подпоследовательность
, следовательно, существует подпоследовательность 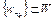 , такая, что
, такая, что 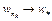 при
при  , где
, где 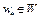 , в силу бикомпактности множества W. Из непрерывности функционала имеем
, в силу бикомпактности множества W. Из непрерывности функционала имеем 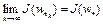 . Так как
. Так как  при
при 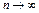 , то
, то 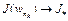 при
при  . Тогда, в силу единственности предельной точки, получим
. Тогда, в силу единственности предельной точки, получим 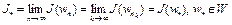 . Итак, доказано соотношение (2). Аналогичным путем можно доказать, что верхняя грань функционала
. Итак, доказано соотношение (2). Аналогичным путем можно доказать, что верхняя грань функционала  достигается в точке
достигается в точке 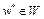 (см. (3)). Теорема доказана.
(см. (3)). Теорема доказана.
Определение 2. Функционал  , определенный на множестве W банахова пространства X, называется полунепрерывным снизу (сверху) в точке
, определенный на множестве W банахова пространства X, называется полунепрерывным снизу (сверху) в точке 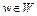 , если для любой последовательности
, если для любой последовательности 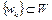 , сильно сходящейся к точке w, имеет место неравенство
, сильно сходящейся к точке w, имеет место неравенство
 .
.
Функционал называется полунепрерывным снизу на множестве W, если он полунепрерывен снизу в каждой точке 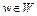 . Функционал
. Функционал  называется непрерывным в точке
называется непрерывным в точке 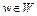 , если он полунепрерывен снизу и сверху в точке w.
, если он полунепрерывен снизу и сверху в точке w.
Теорема 3. Пусть функционал  определен, конечен и полунепрерывен снизу на бикомпактном множестве W. Тогда:
определен, конечен и полунепрерывен снизу на бикомпактном множестве W. Тогда:
1) 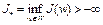 (ограничен снизу);
(ограничен снизу);
2) 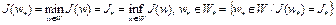 , множество
, множество 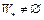 , бикомпактно;
, бикомпактно;
3) любая минимизирующая последовательность 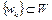 сходится к множеству W*.
сходится к множеству W*.
Доказательство. Пусть 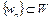 – любая минимизирующая последовательность. Заметим, что минимизирующая последовательность всегда существует (см. лекцию 1). Тогда
– любая минимизирующая последовательность. Заметим, что минимизирующая последовательность всегда существует (см. лекцию 1). Тогда 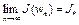 . Поскольку W – бикомпактное множество, то существует подпоследовательность
. Поскольку W – бикомпактное множество, то существует подпоследовательность 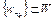 такая, что
такая, что 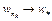 при
при  . Из определения нижней грани и полунепрерывности снизу следует
. Из определения нижней грани и полунепрерывности снизу следует
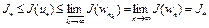 .
.
Отсюда имеем 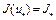 . Следовательно,
. Следовательно, 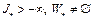 , нижняя грань функционала достигается, любая предельная точка минимизирующей последовательности принадлежит множеству
, нижняя грань функционала достигается, любая предельная точка минимизирующей последовательности принадлежит множеству 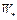 .
.
Покажем, что 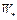 – бикомпактно. Пусть
– бикомпактно. Пусть 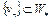 – произвольная последовательность. Так как
– произвольная последовательность. Так как 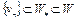 , W – бикомпактно, то существует подпоследовательность
, W – бикомпактно, то существует подпоследовательность  ,
, 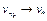 при
при  , причем
, причем  . Заметим, что
. Заметим, что 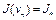 , т.е.
, т.е. 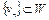 – минимизирующая последовательность. По доказанному выше, предельная точка минимизирующей последовательности принадлежит множеству
– минимизирующая последовательность. По доказанному выше, предельная точка минимизирующей последовательности принадлежит множеству 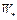 , т.е.
, т.е. 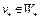 . Это означает, что множество
. Это означает, что множество 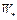 бикомпактно.
бикомпактно.
Покажем, что любая минимизирующая последовательность 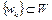 сходится к
сходится к 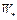 . Следует отметить, что если множество
. Следует отметить, что если множество 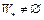 , то существует минимизирующая последовательность, которая сходится к множеству
, то существует минимизирующая последовательность, которая сходится к множеству 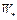 , однако утверждение о том, что любая минимизирующая последовательность сходится к множеству
, однако утверждение о том, что любая минимизирующая последовательность сходится к множеству 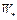 , в общем случае неверно. Поэтому требуется доказательство утверждения 3).
, в общем случае неверно. Поэтому требуется доказательство утверждения 3).
Пусть 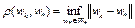 – расстояние от точки
– расстояние от точки 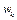 до множества
до множества 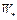 , где
, где 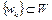 – минимизирующая последовательность. Поскольку
– минимизирующая последовательность. Поскольку 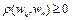 , то
, то 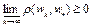 . Так как бикомпактное множество W ограничено, то
. Так как бикомпактное множество W ограничено, то 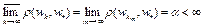 . Подпоследовательность
. Подпоследовательность 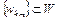 сходится к некоторой точке
сходится к некоторой точке 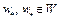 . Так как
. Так как 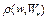 – непрерывный функционал на W, то
– непрерывный функционал на W, то  . По доказанному выше, точка
. По доказанному выше, точка 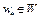 . Тогда
. Тогда 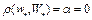 . Следовательно,
. Следовательно, 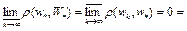
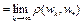 . Теорема доказана.
. Теорема доказана.
Отметим, что в задачах оптимального управления множество W, как правило, является ограниченным и замкнутым множеством. Однако в банаховом пространстве X ограниченности и замкнутости множества W недостаточно для его бикомпактности.
Пример 1. Пусть множество 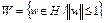 – единичный замкнутый шар в H. Множество W – ограниченное замкнутое множество. Покажем, что W не является бикомпактным множеством. Пусть
– единичный замкнутый шар в H. Множество W – ограниченное замкнутое множество. Покажем, что W не является бикомпактным множеством. Пусть 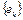 – некоторая бесконечная ортонормированная система в H, т.е.
– некоторая бесконечная ортонормированная система в H, т.е. 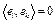 при
при 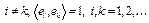 . Заметим, что
. Заметим, что 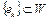 . Покажем, что из последовательности
. Покажем, что из последовательности 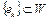 невозможно выбрать подпоследовательность, которая сильно сходится к точке из множества W.
невозможно выбрать подпоследовательность, которая сильно сходится к точке из множества W.
Отметим, что последовательность 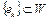 слабо сходится к элементу
слабо сходится к элементу 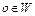 . Напомним, что последовательность
. Напомним, что последовательность 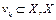 – банахово пространство, слабо сходится к элементу
– банахово пространство, слабо сходится к элементу 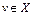 , если
, если 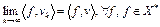 . Для последовательности
. Для последовательности 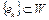 имеем
имеем 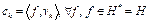 , где
, где 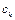 – коэффициенты Фурье элемента f по системе
– коэффициенты Фурье элемента f по системе 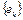 . Согласно неравенству Бесселя, верно неравенство
. Согласно неравенству Бесселя, верно неравенство 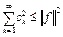 . Отсюда следует, что ряд
. Отсюда следует, что ряд 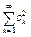 сходится. Следовательно,
сходится. Следовательно, 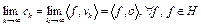 . Это означает, что последовательность
. Это означает, что последовательность 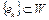 слабо сходится к элементу
слабо сходится к элементу 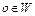 .
.
Предположим, что последовательность 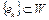 сильно сходится к элементу
сильно сходится к элементу 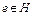 . Тогда последовательность
. Тогда последовательность 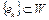 слабо сходится к элементу e. Выше было показано, что
слабо сходится к элементу e. Выше было показано, что 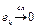 при
при 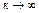 . В силу единственности слабого предела, имеем
. В силу единственности слабого предела, имеем 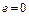 . Тогда
. Тогда 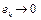 при
при 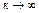 . Следовательно,
. Следовательно, 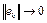 при
при 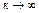 . Это невозможно, так как
. Это невозможно, так как 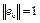 при
при 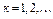 . Значит, множество W не является бикомпактным множеством. Как будет показано ниже, данное множество W является слабо бикомпактным.
. Значит, множество W не является бикомпактным множеством. Как будет показано ниже, данное множество W является слабо бикомпактным.
Поскольку множества W, встречающиеся в задачах оптимального управления, не являются бикомпактными, то теоремы 1–3 невозможно применять для таких задач.
Слабо бикомпактные множества и теорема Вейерштрасса. Рассмотрим задачу оптимального управления (1).
Определение 3. Множество W банахова пространства X называется слабо бикомпактным, если из любой последовательности 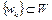 можно выделить хотя бы одну подпоследовательность
можно выделить хотя бы одну подпоследовательность 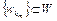 , которая слабо сходится к элементу w, причем
, которая слабо сходится к элементу w, причем 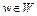 .
.
Определение 4. Функционал  , определенный на множестве W банахова пространства X, слабо полунепрерывен снизу (сверху) в точке
, определенный на множестве W банахова пространства X, слабо полунепрерывен снизу (сверху) в точке 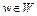 , если для любой последовательности
, если для любой последовательности 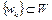 , которая слабо сходится к точке w, выполняется неравенство
, которая слабо сходится к точке w, выполняется неравенство
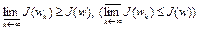 .
.
Функционал  называется слабо полунепрерывным снизу (сверху) на множестве W, если он слабо полунепрерывен снизу (сверху) в каждой точке
называется слабо полунепрерывным снизу (сверху) на множестве W, если он слабо полунепрерывен снизу (сверху) в каждой точке 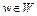 . Функционал слабо непрерывен в точке
. Функционал слабо непрерывен в точке 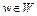 (на множестве W), если он слабо полунепрерывен снизу и сверху в точке w (на множестве W).
(на множестве W), если он слабо полунепрерывен снизу и сверху в точке w (на множестве W).
Определение 5. Последовательность 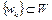 сходится к множеству
сходится к множеству 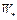 слабо, если
слабо, если 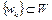 имеет хотя бы одну слабо сходящуюся подпоследовательность, причем слабо предельная точка
имеет хотя бы одну слабо сходящуюся подпоследовательность, причем слабо предельная точка  .
.
Теорема 4. Пусть W – слабо бикомпактное множество банахова пространства X, функционал  определен, конечен и слабо полунепрерывен снизу на W. Тогда:
определен, конечен и слабо полунепрерывен снизу на W. Тогда:
1) 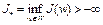 (ограничен снизу);
(ограничен снизу);
2) множество 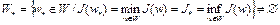 ; слабо бикомпактно;
; слабо бикомпактно;
3) любая минимизирующая последовательность 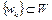 слабо сходится к
слабо сходится к 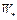 .
.
Доказательство. Пусть 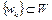 – минимизирующая последовательность, т.е.
– минимизирующая последовательность, т.е. 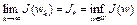 . Так как множество W слабо бикомпактно, то существует подпоследовательность
. Так как множество W слабо бикомпактно, то существует подпоследовательность 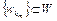 , которая слабо сходится к точке
, которая слабо сходится к точке 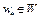 . Из определения нижней грани и слабой полунепрерывности снизу функционала
. Из определения нижней грани и слабой полунепрерывности снизу функционала  на W, имеем
на W, имеем
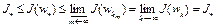 .
.
Отсюда следует, что: 1) 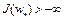 ; 2)
; 2) 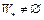 ; 3) любая слабо предельная точка минимизирующей последовательности слабо сходится к
; 3) любая слабо предельная точка минимизирующей последовательности слабо сходится к 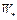 . Следовательно, любая минимизирующая последовательность слабо сходится к
. Следовательно, любая минимизирующая последовательность слабо сходится к 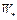 .
.
Покажем, что множество 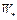 слабо бикомпактно. Пусть
слабо бикомпактно. Пусть 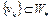 – произвольная последовательность. Так как
– произвольная последовательность. Так как 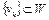 ,
, 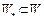 , множество W слабо бикомпактно, то существует подпоследовательность
, множество W слабо бикомпактно, то существует подпоследовательность 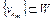 , которая слабо сходится к точке
, которая слабо сходится к точке 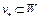 . Из включения
. Из включения 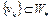 следует, что
следует, что 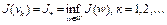 . Следовательно, последовательность
. Следовательно, последовательность 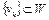 минимизирующая. Тогда, по доказанному выше, точка
минимизирующая. Тогда, по доказанному выше, точка 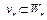 . Это означает, что множество
. Это означает, что множество 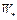 слабо бикомпактно. Теорема доказана.
слабо бикомпактно. Теорема доказана.
Пример 2. Рассмотрим следующую задачу оптимального управления: минимизировать функционал
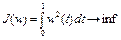
на множестве
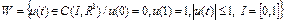 .
.
а) множество W не является бикомпактным множеством. В самом деле, последовательность  , где
, где 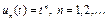 , принадлежит множеству W. Данная последовательность и ее любая подпоследовательность не сходятся к элементу множества W;
, принадлежит множеству W. Данная последовательность и ее любая подпоследовательность не сходятся к элементу множества W;
б) функционал 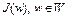 непрерывен. В самом деле, если последовательность
непрерывен. В самом деле, если последовательность 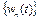 равномерно сходится к элементу
равномерно сходится к элементу 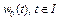 , где
, где 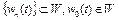 , то
, то 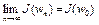 ;
;
в) функционал  не достигает нижней грани на множестве W. Заметим, что для последовательности
не достигает нижней грани на множестве W. Заметим, что для последовательности 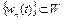 ,
, 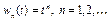 , значение функционала
, значение функционала
Дата добавления: 2015-08-21; просмотров: 1096;
