Глава 7. Краевые задачи оптимального управления………………..226 3 страница
д) докажем оценку (1). Из оценки (2) при фиксированном n, когда 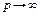 , имеем
, имеем 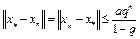 , где
, где 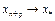 при
при 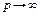 .
.
Теорема доказана.
Отметим, что: 1. Если оператор Ф(x) непрерывно дифференцируем по Фреше на выпуклом замкнутом множестве Q, причем 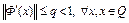 и Ф(x) отображает Q в себя, то справедливы все утверждения теоремы 1. В самом деле, согласно лемме 1 из лекции 1 оператор Ф(x) удовлетворяет условию Липшица
и Ф(x) отображает Q в себя, то справедливы все утверждения теоремы 1. В самом деле, согласно лемме 1 из лекции 1 оператор Ф(x) удовлетворяет условию Липшица 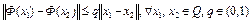 . Это означает, что оператор
. Это означает, что оператор 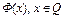 является сжимающим.
является сжимающим.
2. Все утверждения теоремы 1 остаются верными в случае, когда Q=X.
3. Пусть 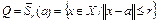 – замкнутый шар и выполнено неравенство
– замкнутый шар и выполнено неравенство 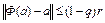 . Тогда, если Ф(x) является сжимающим оператором на
. Тогда, если Ф(x) является сжимающим оператором на 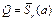 , то верны все утверждения теоремы 1.
, то верны все утверждения теоремы 1.
Легко убедиться в том, что оператор 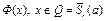 отображает замкнутый шар в себя. Действительно,
отображает замкнутый шар в себя. Действительно,
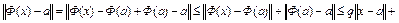
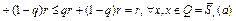 .
.
Следовательно, выполнены все условия теоремы 1.
Пусть оператор Ф(x) отображает множество 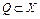 в себя. Тогда оператор
в себя. Тогда оператор 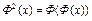 также отображает множество Q в себя. В общем случае для любого натурального числа n оператор
также отображает множество Q в себя. В общем случае для любого натурального числа n оператор 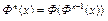 отображает Q в себя. Следующая теорема является обобщением теоремы 1.
отображает Q в себя. Следующая теорема является обобщением теоремы 1.
Теорема 2. Пусть Q замкнутое множество в банаховом пространстве X, оператор Ф(x) отображает Q в себя и для некоторого натурального числа m оператор Фm(x) на Q является сжимающим. Тогда:
1) оператор 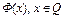 имеет единственную неподвижную точку
имеет единственную неподвижную точку  на Q;
на Q;
2) последовательность 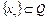 , где
, где  с любой начальной точкой
с любой начальной точкой  , сильно сходится к точке
, сильно сходится к точке  .
.
Доказательство. Рассмотрим оператор 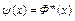 , где m>1. для оператора
, где m>1. для оператора 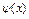 выполнены все условия теоремы 1. Следовательно, оператор
выполнены все условия теоремы 1. Следовательно, оператор 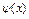 имеет единственную неподвижную точку
имеет единственную неподвижную точку  , где
, где 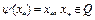 . Так как операторы
. Так как операторы 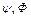 перестановочны, то верны соотношения
перестановочны, то верны соотношения
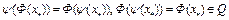 .
.
Отсюда следует, что 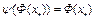 . Это означает, что точка
. Это означает, что точка 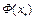 является неподвижной точкой оператора
является неподвижной точкой оператора 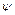 . Так как оператор
. Так как оператор 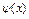 имеет единственную неподвижную точку
имеет единственную неподвижную точку 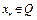 , то должно быть
, то должно быть 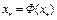 . Следовательно,
. Следовательно, 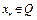 является неподвижной точкой оператора
является неподвижной точкой оператора 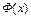 .
.
Покажем, что 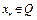 является единственной неподвижной точкой
является единственной неподвижной точкой 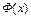 на множестве Q. Предположим противное, т.е. имеется другая неподвижная точка
на множестве Q. Предположим противное, т.е. имеется другая неподвижная точка 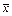 оператора Ф(x), т.е.
оператора Ф(x), т.е. 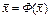 . Заметим, что если
. Заметим, что если 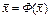 , то
, то 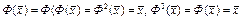 и т.д.
и т.д. 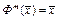 . Следовательно,
. Следовательно, 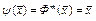 . Тогда
. Тогда 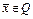 неподвижная точка оператора
неподвижная точка оператора 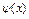 , причем
, причем 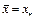 в силу единственности неподвижной точки оператора
в силу единственности неподвижной точки оператора 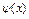 .
.
Второе утверждение следует из теоремы 1. Теорема доказана.
Дифференциальные уравнения. Рассмотрим дифференциальное уравнение следующего вида
 , (3) где
, (3) где 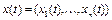 – фазовые координаты объекта управления,
– фазовые координаты объекта управления, 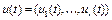 – управление, которое изменяет фазовые координаты,
– управление, которое изменяет фазовые координаты, 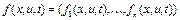 – известная вектор функция, соответствующая устройству объекта управления, t – время.
– известная вектор функция, соответствующая устройству объекта управления, t – время.
В теоретических исследованиях управление 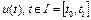 выбирается из функционального пространства
выбирается из функционального пространства 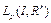 при некотором
при некотором 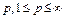 .
.
Норма в пространстве измеримых векторов функции 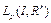 определяется по формуле
определяется по формуле
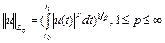 ,
,
а в случае 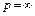
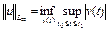 ,
,
где v(t) пробегает множество всех измеримых функций, совпадающих с u(t) почти всюду при 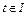 . Имеются ограничения на значения управления в виде
. Имеются ограничения на значения управления в виде
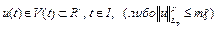 ,
,
где 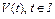 – заданное множество. Например,
– заданное множество. Например, 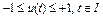 . Таким образом, управление
. Таким образом, управление
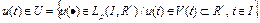 . (4)
. (4)
Для корректности постановки задачи оптимального управления необходимо, чтобы задача Коши (3) при каждом фиксированном  имела единственное решение, исходящее из точки
имела единственное решение, исходящее из точки 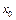 для значений
для значений 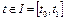 .
.
Заметим, что при фиксированном  , где
, где  , функция
, функция 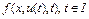 не является непрерывной функцией по t. Поэтому классические теоремы существования и единственности неприменимы.
не является непрерывной функцией по t. Поэтому классические теоремы существования и единственности неприменимы.
Определение 3. Решением дифференциального уравнения (3) при фиксированном  называется непрерывная функция
называется непрерывная функция 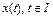 , удовлетворяющая равенству
, удовлетворяющая равенству
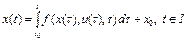 . (5)
. (5)
Рассмотрим в отдельности два случая: 1) 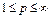 ; 2)
; 2) 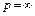 .
.
Теорема 3 (случай 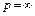 ). Пусть функция
). Пусть функция 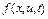 определена и непрерывна по совокупности аргументов
определена и непрерывна по совокупности аргументов 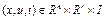 и выполнено условие Липшица
и выполнено условие Липшица
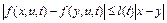 (6)
(6)
при всех  , где
, где 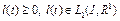 .
.
Тогда: 1) для любого фиксированного  ,
, 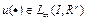 и любого заданного начального условия
и любого заданного начального условия 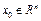 задача (3) имеет, и притом единственное, решение
задача (3) имеет, и притом единственное, решение 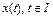 ;
;
2) решение 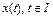 имеет почти всюду производную
имеет почти всюду производную 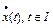 , причем
, причем 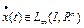 ;
;
3) производная 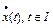 удовлетворяет уравнению (3) при почти всех
удовлетворяет уравнению (3) при почти всех 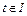 .
.
Доказательство. Поскольку функция 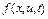 непрерывна по совокупности переменных, а функция
непрерывна по совокупности переменных, а функция 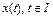 – непрерывна,
– непрерывна,  – ограниченная измеримая функция, то оператор
– ограниченная измеримая функция, то оператор
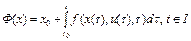
отображает банахово пространство 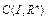 в себя, где
в себя, где 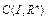 – пространство n-мерных непрерывных функций на отрезке
– пространство n-мерных непрерывных функций на отрезке 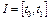 . Так как решение дифференциального уравнения (3) определяется выражением (5), то функция
. Так как решение дифференциального уравнения (3) определяется выражением (5), то функция 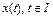 является неподвижной точкой оператора Ф:
является неподвижной точкой оператора Ф:  .
.
Покажем, что оператор 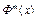 при некотором натуральном числе m является сжимающим. Пусть
при некотором натуральном числе m является сжимающим. Пусть 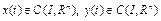 – произвольные элементы из
– произвольные элементы из 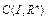 . Докажем, что
. Докажем, что
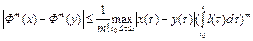 (7)
(7)
при всех 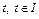 и для любого
и для любого 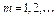 . Для доказательства (7) применим метод математической индукции. Для значения m=1 имеем
. Для доказательства (7) применим метод математической индукции. Для значения m=1 имеем
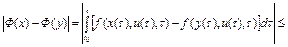
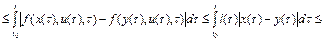
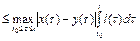 .
.
Отсюда следует, что оценка (7) верна для значения m=1. Пусть оценка (7) верна для натурального числа m>1. Покажем, что она верна для значений m+1. В самом деле,
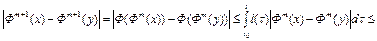
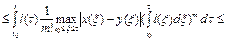
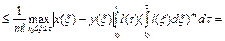
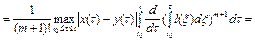
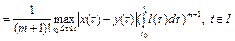 .
.
Итак, верна оценка (7). Так как оценка (7) верна для всех 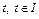 , то
, то

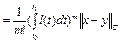 .
.
Поскольку 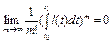 , то найдется натуральное число m>1 такое, что величина
, то найдется натуральное число m>1 такое, что величина
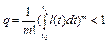 .
.
Тогда для такого значения m имеем 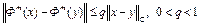 . Это означает, что оператор
. Это означает, что оператор 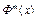 является сжимающим. Тогда согласно теореме 2 оператор Ф(x) имеет единственную неподвижную точку
является сжимающим. Тогда согласно теореме 2 оператор Ф(x) имеет единственную неподвижную точку 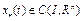 , т.е.
, т.е.
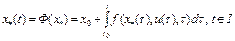 .
.
Следовательно, интегральное уравнение (5) имеет единственное решение 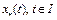 .
.
Заметим, что если оператор Ф(x) отображает 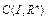 в себя, то для любого m>1 оператор
в себя, то для любого m>1 оператор 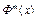 отображает
отображает 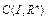 в себя. Так как
в себя. Так как 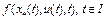 ограниченная измеримая функция, то
ограниченная измеримая функция, то 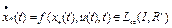 и почти всюду удовлетворяет уравнению (3). Теорема доказана.
и почти всюду удовлетворяет уравнению (3). Теорема доказана.
Теорема 4 (случай 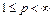 ). Пусть выполнены условия теоремы 3, и пусть, кроме того
). Пусть выполнены условия теоремы 3, и пусть, кроме того
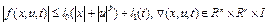 , (8) где
, (8) где 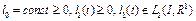 . Тогда:
. Тогда:
1) для любого фиксированного 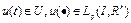 и любого заданного
и любого заданного 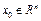 начальная задача Коши (3) имеет, и притом единственное, решение
начальная задача Коши (3) имеет, и притом единственное, решение 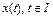 ;
;
2) решение 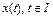 имеет почти всюду производную
имеет почти всюду производную 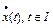 , причем
, причем 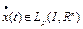 ;
;
3) производная 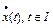 удовлетворяет условию (3) при почти всех
удовлетворяет условию (3) при почти всех 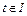 .
.
Доказательство. Доказательство теоремы аналогично доказательству теоремы 2.
При выполнении условия (8) существует интеграл
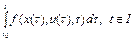 ,
,
оператор
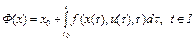
отображает 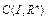 в себя и для некоторого натурального числа m>1 оператор
в себя и для некоторого натурального числа m>1 оператор 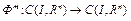 является сжимающим. Теорема доказана.
является сжимающим. Теорема доказана.
По теоремам существования и единственности решения дифференциальных уравнений в банаховом пространстве рекомендуется литература: Алексеев В. М., Тихомиров В. М., Фомин С. В. Оптимальное управление. – М.: Наука, 1979.
ЛЕКЦИЯ 4.ИТЕРАЦИОННЫЙ ПРОЦЕСС НЬЮТОНА-КАНТОРОВИЧА
Дифференцирование нелинейных операторов позволяет с помощью локальной аппроксимации нелинейных операторов установить связь с линейными операторами. Далее, используя результаты теории линейных операторов, можно предложить метод решения нелинейных функциональных уравнений. Примечательно то, что метод Ньютона-Канторовича дает условия существования, единственности и область расположения решения функциональных уравнений до построения их решения.
Алгоритм итерационного процесса. Пусть оператор F(x) переводит открытое множество S банахова пространства X в банахово пространство Y. Предположим, в S имеется решение операторного уравнения F(x)=0. Строим последовательность 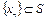 по алгоритму:
по алгоритму:
1. Выбирается начальное приближение 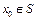 ;
;
2. Вычислим производную Фреше оператора F(x) в точке 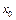 . В результате находим линейный ограниченный оператор
. В результате находим линейный ограниченный оператор 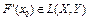 ;
;
3. Вычислим обратный оператор 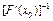 ;
;
4. Следующее приближение 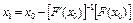 . В общем случае
. В общем случае  .
.
Сходимость итерационного процесса. На практике для решения функциональных уравнений F(x)=0 часто применяется следующая теорема.
Теорема 1. Пусть выполнены следующие условия:
1) оператор F(x) дифференцируем по Фреше в шаре 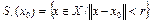 , причем
, причем
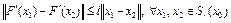 ; (2)
; (2)
2) существует непрерывный обратный оператор 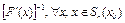 , причем
, причем
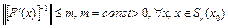 ; (3)
; (3)
3) 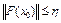 , величина
, величина 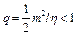 ,
,
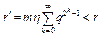 . (4)
. (4)
Тогда уравнение F(x)=0 имеет решение 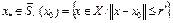 , последовательность
, последовательность 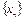 , определяемая по формуле (1), сходится к элементу
, определяемая по формуле (1), сходится к элементу  . Справедлива следующая оценка скорости сходимости
. Справедлива следующая оценка скорости сходимости
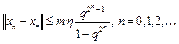 . (5)
. (5)
Доказательство. Итерационный процесс (1) запишем в виде
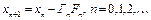 , (6) где
, (6) где 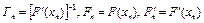 .
.
а) покажем, что 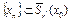 . Для доказательства данного включения применим метод математической индукции. Для значений n=1 из (6) имеем
. Для доказательства данного включения применим метод математической индукции. Для значений n=1 из (6) имеем 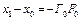 . Тогда
. Тогда 
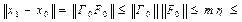
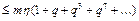 . Так как
. Так как 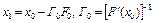 , то
, то 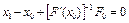 . Следовательно,
. Следовательно, 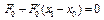 , где
, где 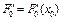 .
.
Тогда
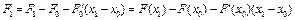 ,
,
где 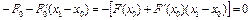 .
.
Поскольку 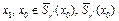 – выпуклое множество и выполнено неравенство (2), то, согласно лемме 2, лекция 2 (см. (7)), имеем
– выпуклое множество и выполнено неравенство (2), то, согласно лемме 2, лекция 2 (см. (7)), имеем 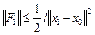 . Таким образом, для значения n=1 верны неравенства
. Таким образом, для значения n=1 верны неравенства
 .
.
Полагаем, что для значений n>1 верны оценки
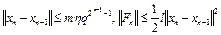 . (7)
. (7)
Покажем, что для значений n+1 верны неравенства
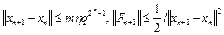 . (8)
. (8)
Как следует из (6), разность 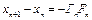 . Тогда (см. (3), (4))
. Тогда (см. (3), (4))
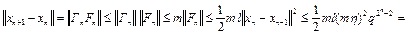
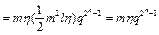 ,
,
в силу оценки (7). Так как 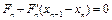 , то
, то
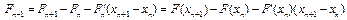 .
.
Отсюда, с учетом оценки (7) из лекции 2, имеем
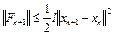 .
.
Итак, доказаны оценки (8) для значений n+1. Из оценки (8) следует, что
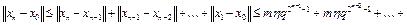
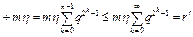 .
.
Тогда 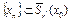 .
.
б) докажем, что последовательность 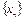 – фундаментальна. Для любого натурального числа p верна оценка (см. (8))
– фундаментальна. Для любого натурального числа p верна оценка (см. (8))
 . (9)
. (9)
Отсюда следует, что 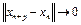 при
при 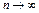 для любого натурального числа p. Следовательно, последовательность
для любого натурального числа p. Следовательно, последовательность 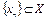 – фундаментальна. Так как пространство X банахово, то последовательность
– фундаментальна. Так как пространство X банахово, то последовательность 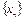 сходится, т.е.
сходится, т.е. 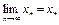 . Поскольку
. Поскольку 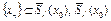 – замкнутый шар, то
– замкнутый шар, то 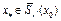 .
.
в) докажем, что точка 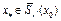 – решение операторного уравнения F(x)=0. Из (1) (либо (6)), переходя к пределу при
– решение операторного уравнения F(x)=0. Из (1) (либо (6)), переходя к пределу при 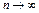 , получим
, получим 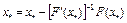 . Отсюда имеем
. Отсюда имеем 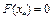 . Следовательно,
. Следовательно, 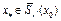 – решение операторного уравнения F(x)=0.
– решение операторного уравнения F(x)=0.
г) докажем оценку (5). Из (9) при 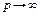 , с учетом того, что
, с учетом того, что 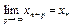 , имеем
, имеем
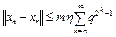 . (10) Так как
. (10) Так как
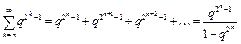 ,
,
то из (10) получим
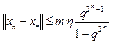 .
.
Теорема доказана.
Модифицированный метод Ньютона. Как следует из формулы (1), необходимо для каждой итерации вычислить обратный оператор 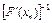 . Вычисление обратных операторов
. Вычисление обратных операторов 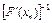 ,
, 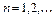 довольно сложная задача. Поэтому целесообразно построение последовательности
довольно сложная задача. Поэтому целесообразно построение последовательности 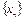 по алгоритму
по алгоритму
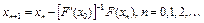 , (11) где обратный оператор
, (11) где обратный оператор 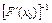 вычисляется только один раз.
вычисляется только один раз.
Теорема 2. Пусть выполнены следующие условия:
1) оператор F(x) дифференцируем по Фреше в открытом шаре 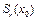 банахова пространства X, причем
банахова пространства X, причем
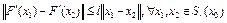 ;
;
2) оператор 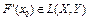 непрерывно обратим,
непрерывно обратим, 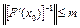 ;
;
3) 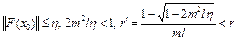 .
.
Тогда уравнение F(x)=0 имеет единственное решение 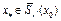 , последовательность
, последовательность 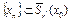 , определяемая по формуле (11) с начальной точкой
, определяемая по формуле (11) с начальной точкой 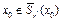 , сходится к точке
, сходится к точке  . Справедлива следующая оценка скорости сходимости
. Справедлива следующая оценка скорости сходимости
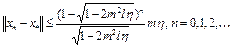 .
.
Доказательство. Введем оператор 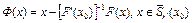 .
.
а) покажем, что оператор Ф(x) отображает 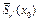 в себя. Для этого достаточно показать, что
в себя. Для этого достаточно показать, что  . Действительно,
. Действительно, 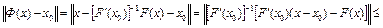
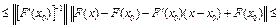
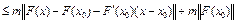 .
.
Отсюда с учетом того, что
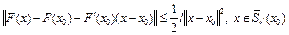 , получим
, получим
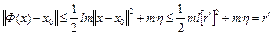 .
.
Величина 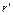 является наименьшим корнем квадратного уравнения
является наименьшим корнем квадратного уравнения 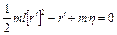 . Отсюда следует величина
. Отсюда следует величина
 . (12)
. (12)
Таким образом, если 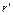 определяется по формуле (12), то верно неравенство
определяется по формуле (12), то верно неравенство 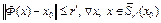 . Это означает, что оператор Ф(x) отображает
. Это означает, что оператор Ф(x) отображает 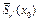 в себя.
в себя.
Дата добавления: 2015-08-21; просмотров: 955;
